题目内容
16. 如图,对任意的五角星,结论正确的是( )
如图,对任意的五角星,结论正确的是( )| A. | ∠A+∠B+∠C+∠D+∠E=90° | B. | ∠A+∠B+∠C+∠D+∠E=180° | ||
| C. | ∠A+∠B+∠C+∠D+∠E=270° | D. | ∠A+∠B+∠C+∠D+∠E=360° |
分析 根据三角形的一个外角等于和它不相邻的两个内角的和得到∠1=∠2+∠D,∠2=∠A+∠C,根据三角形内角和定理得到答案.
解答 解:∵∠1=∠2+∠D,
∠2=∠A+∠C,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
故选:B.
点评 本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如果不等式组$\left\{\begin{array}{l}{-4x+1<-8-x}\\{x>m}\end{array}\right.$的解集是x>m,那么m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m=3 | D. | m<3 |
5. 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
 如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )
如图,△ABC≌△EFD,AB∥EF,DF∥BC,则∠B的对应角是( )| A. | ∠F | B. | ∠FDE | C. | ∠E | D. | 以上都不正确 |
6.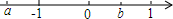 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
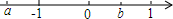 已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )
已知a,b在数轴上的位置如图所示,则化简|a+b|+$\sqrt{(a-b)^{2}}$的结果为( )| A. | -2a | B. | 2b | C. | -2b | D. | 2a |
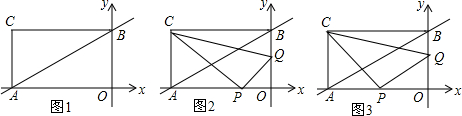
 如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm.
如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm.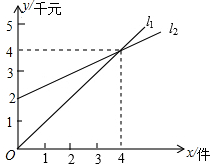 如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.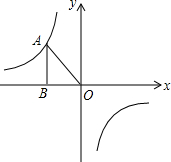 已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.
已知如图,反比例函数y=-$\frac{6}{x}$的图象上有一点A(-2,■),它的纵坐标被墨水污染了,根据题意,解答下列问题.