题目内容
7.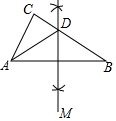 如图,在△ABC中,∠C=90°,∠B=30°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,连接AD,则cos∠CDA=$\frac{1}{2}$.
如图,在△ABC中,∠C=90°,∠B=30°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,连接AD,则cos∠CDA=$\frac{1}{2}$.
分析 由线段垂直平分线的性质得出AD=BD,得出∠DAB=∠B=30°,由三角形的外角性质得出∠CDA=60°,即可得出结果.
解答 解:根据题意得:MD是线段AB的垂直平分线,
∴AD=BD,
∴∠DAB=∠B=30°,
∴∠CDA=∠DAB+∠B=60°,
∴cos∠CDA=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 此题主要考查了基本作图、线段垂直平分线的性质、等腰三角形的性质、三角形的外角性质以及三角函数,正确掌握线段垂直平分线的性质是解题关键.

练习册系列答案
相关题目
17. 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )
 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )| A. |  | B. |  | C. |  | D. |  |
18.下列图形中由AB∥CD能得到∠1=∠2的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
15.-2017的绝对值是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
12.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-2ab)2=4a2b2 | D. | 3a2b2÷a2b2=3ab |
2.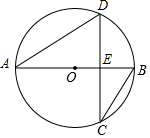 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )| A. | 3$\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $5\sqrt{3}$ | D. | $6\sqrt{3}$ |
 已知反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b的图象可能是( )
已知反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b的图象可能是( )


