题目内容
2.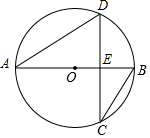 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )| A. | 3$\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $5\sqrt{3}$ | D. | $6\sqrt{3}$ |
分析 连结OC,AC,先根据直角的性质得到∠ABC的度数,再圆周角定理得到∠AOC的度数,根据等边三角形的性质和垂径定理得到⊙O的半径和直径,再解直角三角形即可求解.
解答  解:连结OC,AC,
解:连结OC,AC,
∵弦DC垂直AB于点E,∠DCB=30°,
∴∠ABC=60°,
∴△BOC是等边三角形,
∵EB=3,
∴OB=6,
∴AB=12,
AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB,AC=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$.
故选:D.
点评 此题考查了垂径定理,圆周角定理以及等边三角形的性质,注意掌握数形结合思想的应用.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
8.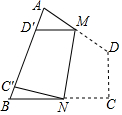 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
12.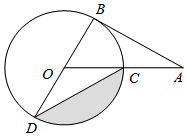 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )| A. | $\frac{4}{3}π-\sqrt{3}$ | B. | $\frac{4}{3}π-2\sqrt{3}$ | C. | $4π-4\sqrt{3}$ | D. | $\frac{16}{3}π-4\sqrt{3}$ |
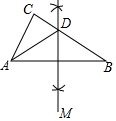 如图,在△ABC中,∠C=90°,∠B=30°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,连接AD,则cos∠CDA=$\frac{1}{2}$.
如图,在△ABC中,∠C=90°,∠B=30°,分别以点A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,连接AD,则cos∠CDA=$\frac{1}{2}$. 如图,在△ABC中,∠ABC=60°,AB=6,BC=10,以AC为边在△ABC外作等边△ACD,则BD的长为14.
如图,在△ABC中,∠ABC=60°,AB=6,BC=10,以AC为边在△ABC外作等边△ACD,则BD的长为14.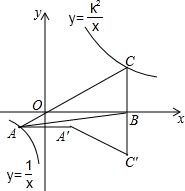 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10.