题目内容
15.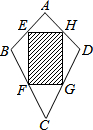 某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )
某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )| A. | 15匹 | B. | 20匹 | C. | 60匹 | D. | 30匹 |
分析 连接AC、BD,根据三角形中位线定理证明△BEF∽△BAC,且相似比为1:2,则面积比为1:4,同理证明阴影部分面积等于如图所示的风筝面积的一半,得到答案.
解答 解: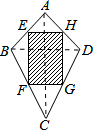 连接AC、BD,
连接AC、BD,
∵点E、F分别是AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
∴△BEF∽△BAC,
∴S△BEF=$\frac{1}{4}$S△BAC,
同理,S△DHG=$\frac{1}{4}$S△DAC,
则S△BEF+S△DHG=$\frac{1}{4}$S△BAC+$\frac{1}{4}$S△DAC=$\frac{1}{4}$S四边形ABCD,
同理S△AEH+S△CFG=$\frac{1}{4}$S四边形ABCD,
∴阴影部分面积等于如图所示的风筝面积的一半,
即阴影部分面积与其余部分面积相等,
生产这批风筝需要甲布料30匹,那么需要乙布料也是30匹,
故选:D.
点评 本题考查的是中点四边形的知识,掌握三角形中位线定理和相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
6.一张长方形彩板用下列方法可以载剪出A、B、C三种零件
如表表示组装一个甲(乙)模型所需要的零件数量
(1)3张长方形彩板用方法1可以载剪出A种零件6个;
(2)若用25张长方形彩板载剪的A、B两种零件,恰好能全部用于甲模型的组装,请你通过计算确定载剪的方法;
(3)已知一个甲模型和一个乙模型可包装成一套产品,用122张长方形彩板最多能生产包装多少套产品?
| A(个) | B(个) | C(个) | |
| 方法1 | 2 | 0 | 0 |
| 方法2 | 0 | 6 | 0 |
| 方法3 | 0 | 2 | 2 |
| A(个) | B(个) | C(个) | |
| 甲模型(个) | 1 | 2 | 0 |
| 乙模型(个) | 0 | 1 | 1 |
(2)若用25张长方形彩板载剪的A、B两种零件,恰好能全部用于甲模型的组装,请你通过计算确定载剪的方法;
(3)已知一个甲模型和一个乙模型可包装成一套产品,用122张长方形彩板最多能生产包装多少套产品?
10.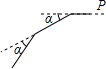 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
4.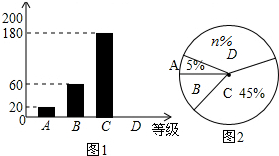 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有400人,m=15%,n=35.
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
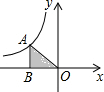 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$. ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“
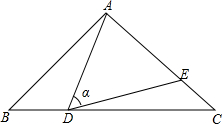 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论: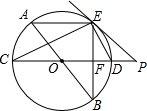 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.