题目内容
14.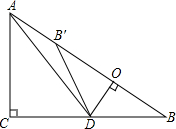 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
分析 (1)由∠DOB=∠ACB=90°,∠B=∠B,容易证明△DOB∽△ACB;
(2)先由勾股定理求出AB,由角平分线的性质得出DC=DO,再由HL证明Rt△ACD≌Rt△AOD,得出AC=AO,设BD=x,则DC=DO=8-x,由勾股定理得出方程,解方程即可;
(3)根据题意得出当△AB′D为等腰三角形时,AB′=DB′,由△DOB∽△ACB,得出$\frac{OB}{BD}=\frac{BC}{AB}$=$\frac{4}{5}$,设BD=5x,则AB′=DB′=5x,BO=B′O=4x,由AB′+B′O+BO=AB,得出方程,解方程求出x,即可得出BD.
解答 (1)证明:∵DO⊥AB,
∴∠DOB=∠DOA=90°,
∴∠DOB=∠ACB=90°,
又∵∠B=∠B,
∴△DOB∽△ACB;
(2)解:∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AD平分∠CAB,DC⊥AC,DO⊥AB,
∴DC=DO,
在Rt△ACD和Rt△AOD中,
$\left\{\begin{array}{l}{AD=AD}\\{DC=DO}\end{array}\right.$,
∴Rt△ACD≌Rt△AOD(HL),
∴AC=AO=6,
设BD=x,则DC=DO=8-x,OB=AB-AO=4,
在Rt△BOD中,根据勾股定理得:DO2+OB2=BD2,
即(8-x)2+42=x2,
解得:x=5,
∴BD的长为5;
(3)解:∵点B′与点B关于直线DO对称,
∴∠B=∠OB′D,BO=B′O,BD=B′D,
∵∠B为锐角,
∴∠OB′D也为锐角,
∴∠AB′D为钝角,
∴当△AB′D为等腰三角形时,AB′=DB′,
∵△DOB∽△ACB,
∴$\frac{OB}{BD}=\frac{BC}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$,
设BD=5x,
则AB′=DB′=5x,BO=B′O=4x,
∵AB′+B′O+BO=AB,
∴5x+4x+4x=10,
解得:x=$\frac{10}{13}$,
∴BD=$\frac{50}{13}$.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、勾股定理、全等三角形的判定与性质、角平分线的性质等知识;本题难度较大,综合性强,特别是(2)(3)中,需要根据题意列出方程,解方程才能得出结果.

| A. | 调查方式是抽样调查 | |
| B. | 该校只有360个家长持反对态度 | |
| C. | 样本是400个家长对“中学生骑电动车上学”的态度 | |
| D. | 该校约有90%的家长持反对态度 |
 如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.
如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC. 如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.
如图,四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为3.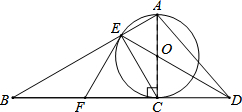 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.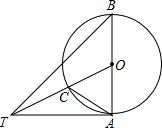 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.