题目内容
6. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.
分析 根据正方形的性质得出∠BAE=∠DAE,再利用SAS证明△ABE与△ADE全等,再利用三角形的内角和解答即可.
解答 解:∵正方形ABCD,
∴AB=AD,∠BAE=∠DAE,
在△ABE与△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAE}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ADE(SAS),
∴∠AEB=∠AED,∠ABE=∠ADE,
∵∠CBF=20°,
∴∠ABE=70°,
∴∠AED=∠AEB=180°-45°-70°=65°,
故答案为:65
点评 此题考查正方形的性质,关键是根据正方形的性质得出∠BAE=∠DAE,再利用全等三角形的判定和性质解答.

练习册系列答案
相关题目
17.1号探测气球从海拔5m处出发,以lm/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都匀速上升了50min.
设气球球上升时间为xmin (0≤x≤50)
(Ⅰ)根据题意,填写下表:
(Ⅱ)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;
(Ⅲ)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
设气球球上升时间为xmin (0≤x≤50)
(Ⅰ)根据题意,填写下表:
| 上升时间/min | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/m | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/m | 20 | 30 | … | 0.5x+15 |
(Ⅲ)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
1.9的平方根是( )
| A. | ±3 | B. | ±$\frac{1}{3}$ | C. | 3 | D. | -3 |
18.2015年某中学举行的春季田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A. | 1.70m,1.65m | B. | 1.70m,1.70m | C. | 1.65m,1.60m | D. | 3,4 |
15. 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )
 如图所示的几何体为圆台,其俯视图正确的是( )
如图所示的几何体为圆台,其俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |

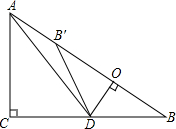 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.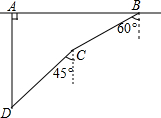 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).