题目内容
9.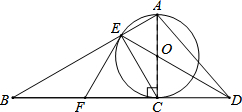 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
分析 (1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
解答 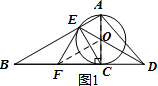 证明:(1)如图1,连接FO,
证明:(1)如图1,连接FO,
∵F为BC的中点,AO=CO,
∴OF∥AB,
∵AC是⊙O的直径,
∴CE⊥AE,
∵OF∥AB,
∴OF⊥CE,
∴OF所在直线垂直平分CE,
∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠0EC=∠0CE,
∵∠ACB=90°,
即:∠0CE+∠FCE=90°,
∴∠0EC+∠FEC=90°,
即:∠FEO=90°,
∴FE为⊙O的切线;
(2)如图2,∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴∠EOA=60°,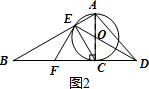
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=$3\sqrt{3}$,
∵在Rt△ACD中,∠ACD=90°,
CD=$3\sqrt{3}$,AC=6,
∴AD=$3\sqrt{7}$.
点评 本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,熟练掌握定理是解题的关键.

练习册系列答案
相关题目
19. 如图,一定能判定AD∥BC的是 ( )
如图,一定能判定AD∥BC的是 ( )
 如图,一定能判定AD∥BC的是 ( )
如图,一定能判定AD∥BC的是 ( )| A. | ∠1=∠4 | B. | ∠2=∠4 | C. | ∠3=∠4+∠5 | D. | ∠3=∠5 |
17.1号探测气球从海拔5m处出发,以lm/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都匀速上升了50min.
设气球球上升时间为xmin (0≤x≤50)
(Ⅰ)根据题意,填写下表:
(Ⅱ)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;
(Ⅲ)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
设气球球上升时间为xmin (0≤x≤50)
(Ⅰ)根据题意,填写下表:
| 上升时间/min | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/m | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/m | 20 | 30 | … | 0.5x+15 |
(Ⅲ)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
1.9的平方根是( )
| A. | ±3 | B. | ±$\frac{1}{3}$ | C. | 3 | D. | -3 |
18.2015年某中学举行的春季田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
这些运动员跳高成绩的中位数和众数分别是( )
| 成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A. | 1.70m,1.65m | B. | 1.70m,1.70m | C. | 1.65m,1.60m | D. | 3,4 |
 已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图: 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA1=1,则OA2015的长为22014.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA1=1,则OA2015的长为22014.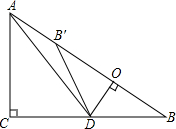 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD. 如图是由5个相同的正方形组成的几何体的左视图和俯视图,则该几何体的主视图不可能是( )
如图是由5个相同的正方形组成的几何体的左视图和俯视图,则该几何体的主视图不可能是( )


