题目内容
(1)如图1,如果AB∥ED,证明:∠C=∠B+∠D.
(2)如图2,如果∠C=∠B+∠D,AB、ED是否平行?证明你的结论.

(2)如图2,如果∠C=∠B+∠D,AB、ED是否平行?证明你的结论.

考点:平行线的判定与性质
专题:
分析:(1)先过C作CF∥AB,根据平行于同一直线的两直线平行得出AB∥CF∥ED,再根据平行线的性质得出∠FCD=∠D和∠B=∠BCF,从而得出∠C=∠B+∠D;
(2)过C作CF∥AB,得出∠BCF=∠B,再根据∠C=∠BCF+∠DCF=∠B+∠DCF和∠C=∠B+∠D,得出∠DCF=∠D,再根据平行线的判定得出CF∥ED,从而证出AB∥ED.
(2)过C作CF∥AB,得出∠BCF=∠B,再根据∠C=∠BCF+∠DCF=∠B+∠DCF和∠C=∠B+∠D,得出∠DCF=∠D,再根据平行线的判定得出CF∥ED,从而证出AB∥ED.
解答: 解:(1)过C作CF∥AB,
解:(1)过C作CF∥AB,
∵AB∥ED,
∴CF∥ED,
∴∠FCD=∠D,
∵AB∥ED,
∴∠B=∠BCF,
∴∠BCF+∠FCD=∠B+∠D,
∴∠C=∠B+∠D;
(2)过C作CF∥AB,
则∠BCF=∠B,
∵∠C=∠BCF+∠DCF=∠B+∠DCF,
又∵∠C=∠B+∠D,
∴∠DCF=∠D,
∴CF∥ED,
∴AB∥ED.
 解:(1)过C作CF∥AB,
解:(1)过C作CF∥AB,∵AB∥ED,
∴CF∥ED,
∴∠FCD=∠D,
∵AB∥ED,
∴∠B=∠BCF,
∴∠BCF+∠FCD=∠B+∠D,
∴∠C=∠B+∠D;
(2)过C作CF∥AB,

则∠BCF=∠B,
∵∠C=∠BCF+∠DCF=∠B+∠DCF,
又∵∠C=∠B+∠D,
∴∠DCF=∠D,
∴CF∥ED,
∴AB∥ED.
点评:此题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 如图,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长为多少?
如图,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长为多少? 定义新运算“对于任意实数a、b,都有a?b=
定义新运算“对于任意实数a、b,都有a?b=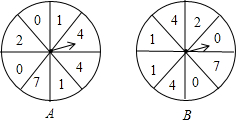 北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下:
北京时间2014年6月30日凌晨,来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军,如图两个可以自由转动的转移A、B,每个转盘被分成8个相等的扇形,其规则如下: 两个大小不同的等边△ABC和等边△DEC如图摆放,连接AE、BD,M、N、P、Q分别为线段AB、BD、ED、AE的中点.
两个大小不同的等边△ABC和等边△DEC如图摆放,连接AE、BD,M、N、P、Q分别为线段AB、BD、ED、AE的中点.