题目内容
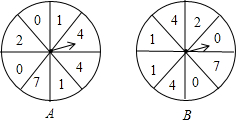北京时间2014年6月30日凌晨，来自巴西和德国的球迷Oscar和Kroos利用“争1点”的游戏来预测2014年巴西世界杯冠军，如图两个可以自由转动的转移A、B，每个转盘被分成8个相等的扇形，其规则如下：①Oscar自由转动转盘A，同时Kroos自由转动转盘B；
②转盘停止后，指针指向几就顺时针走几格，得到一个数字（若转盘A中指针指向2，则按顺时针方向走2格得到数字1）；
③若最终得到的数字是1，则自己的祖国为预测冠军（若双方都得到1，则重新开始）．
这个游戏对双方公平吗？请说明理由．
考点：游戏公平性
专题：计算题
分析：列表得出所有等可能的情况数，找出Oscar和Kroos获胜的情况，求出各自的概率，比较即可．
解答：解：这个游戏公平，理由为：
列表如下：
所有等可能的情况有64种，其中Oscar获胜的情况有（1，0），（1，7），（1，0），（1，4），（1，4），（1，2），（1，0），（1，7），（1，0），（1，4），（1，4），（1，2）共12种，Kroos获胜的情况有：（4，1），（4，1），（4，1），（4，1），（7，1），（7，1），（0，1），（0，1），（2，1），（2，1），（0，1），（0，1）共12种，
∴P（Oscar获胜）=P（Kroos获胜）=
=
，
则这个游戏公平．
列表如下：
| 4 | 4 | 1 | 7 | 0 | 2 | 0 | 1 | |
| 0 | （4，0） | （4，0） | （1，0） | （7，0） | （0，0） | （2，0） | （0，0） | （1，0） |
| 7 | （4，7） | （4，7） | （1，7） | （7，7） | （0，7） | （2，7） | （0，7） | （1，7） |
| 0 | （4，0） | （4，0） | （1，0） | （7，0） | （0，0） | （2，0） | （0，0） | （1，0） |
| 4 | （4，4） | （4，4） | （1，4） | （7，4） | （0，4） | （2，4） | （0，4） | （1，4） |
| 1 | （4，1） | （4，1） | （1，1） | （7，1） | （0，1） | （2，1） | （0，1） | （1，1） |
| 1 | （4，1） | （4，1） | （1，1） | （7，1） | （0，1） | （2，1） | （0，1） | （1，1） |
| 4 | （4，4） | （4，4） | （1，4） | （7，4） | （0，4） | （2，4） | （0，4） | （1，4） |
| 2 | （4，2） | （4，2） | （1，2） | （7，2） | （0，2） | （2，2） | （0，2） | （1，2） |
∴P（Oscar获胜）=P（Kroos获胜）=
| 12 |
| 64 |
| 3 |
| 16 |
则这个游戏公平．
点评：此题考查了列表法与树状图法，用到的知识有：事件的概率=发生的情况数÷所有等可能情况数．
练习册系列答案
阅读快车系列答案
相关题目
如图，点A在∠O的一边OA上．按要求画图并填空：
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE=1.7m，斜面坡角为35°，求木箱端点E距地面AC的高度EF．（精确到0.1米）
如图，在?ABCD中，已知两条对角线相交于点O，E、F、G、H分别是AO、BO、CO、DO的中点，以图中的点为顶点，尽可能多地画出平行四边形．
如图，∠AOB是平角，射线OD平分∠AOC，射线OE平分∠BOD，且∠BOC=4∠AOD，求∠COE的度数．