题目内容
18.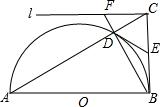 如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.
如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.(1)求证:点E是BC的中点;
(2)过点C作AB的平行线l,l与BD的延长线交于点F,若$\frac{FD}{DB}$=$\frac{1}{3}$,求∠BAC的度数.
分析 (1)根据切线长定理得到ED=EB,再根据等角的余角相等证明∠EDC=∠ECD,得到ED=EC由此即可证明.
(2))由CF∥AB,得$\frac{DF}{DB}$=$\frac{CD}{AD}$=$\frac{1}{3}$,设CD=a,AD=3a,由△ADB∽△BDC,得$\frac{AD}{BD}$=$\frac{BD}{DC}$,求出BD,再求出tan∠BAD的值即可解决问题.
解答 (1)证明:∵AB是直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴BC⊥AB,
∴BC是⊙O的切线,
∵ED、EB是⊙O的切线,
∴ED=EB,
∴∠EDB=∠EBD,
∵∠EBD+∠BCD=90°,∠EDC+∠EDB=90°,
∴∠ECD=∠EDC,
∴EC=EB,
∴点E是BC中点.
(2)∵CF∥AB,
∴$\frac{DF}{DB}$=$\frac{CD}{AD}$=$\frac{1}{3}$,设CD=a,AD=3a,
∵∠DAB+∠ABD=90°,∠ABD+∠DBC=90°,
∴∠DAB=∠DBC,∵∠ADB=∠BDC=90°,
∴△ADB∽△BDC,
∴$\frac{AD}{BD}$=$\frac{BD}{DC}$,
∴BD2=DA•DC=3a2,
∵BD>0,
∴BD=$\sqrt{3}$a,
∴tan∠BAD=$\frac{BD}{AD}$=$\frac{\sqrt{3}}{3}$,
∴∠BAD=30°即∠BAC=30°.
点评 本题考查切线的性质、平行线分线段成比例定理、三角函数定义等知识,解题的关键是灵活运用等角的余角相等证明角相等,学会设参数表示相应的线段解决问题,属于中考常考题型.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.已知一次函数y=kx+3经过点(2,1),则一次函数的图象经过的象限是( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
19.下列计算正确的是( )
| A. | 2a2-4a2=-2 | B. | 3a+a=3a2 | C. | 5b•b=5b2 | D. | 4a6÷2a3=2a2 |
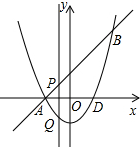 如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.
如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.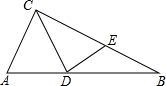 如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.
如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.