题目内容
7.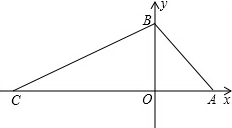 如图,在平面直角坐标系中,O为坐标原点,直线AB与x轴交于点A,与y轴交于点B,且A(4,0),B(0,4),点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).
如图,在平面直角坐标系中,O为坐标原点,直线AB与x轴交于点A,与y轴交于点B,且A(4,0),B(0,4),点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).(1)求点C的坐标.
(2)连接BP,分别过点A,C向直线BP作垂线,垂足分别为E,F,线段EF的垂直平分线交AC于点G,连接BG,延长EG,CF交于点Q,求OG的长.
分析 (1)根据函数解析式y=-x+4,令x=0得:y=4,于是得到B(0,4),根据已知条件S△ABC=28,求得AC=14,即可得到结论;
(2)连接EG并延长交直线CF于点Q,求出EG=QG,∠GCQ=∠EAG,根据AAS证△GCQ≌△GAE,推出CG=AG,求出GA=7,OG=3.
解答 解:(1)∵y=-x+4,
令x=0得:y=4,
∴B(0,4),
∵S△ABC=28,
∴S△ABC=$\frac{1}{2}$AC•OB,
∴AC=14,
∴OC=10,
∴C(-10,0);
(2)连接EG并延长交直线CF于点Q,如图1,
∵CQ∥MG∥AE,ME=MF,
∴EG=QG,∠GCQ=∠EAG,
在△GCQ和△GAE中
$\left\{\begin{array}{l}{∠GCQ=∠EAG}\\{∠CGQ=∠AGE}\\{EG=GO}\end{array}\right.$
∴△GCQ≌△GAE,
∴CG=AG,
∴GA=$\frac{1}{2}$AC=7,
∴OG=GA-OA=7-4=3.
点评 本题考查了勾股定理,全等三角形的性质和判定,三角形的面积,主要考查学生综合运用性质进行计算的能力,题目综合性比较强,正确的作出图形是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.单项式-x2y的系数和次数分别是( )
| A. | 0,2 | B. | 0,3 | C. | -1,3 | D. | -1,2 |
19.下面四个数中,负数是( )
| A. | 20 | B. | 0 | C. | 3 | D. | -2 |
16.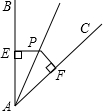 如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
 如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
如图点P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )| A. | HL | B. | ASA | C. | AAS | D. | SAS |
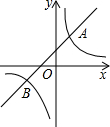 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.