题目内容
12.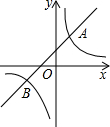 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(1,3),B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)点C为x轴正半轴上一点,连接AO,AC,且AO=AC,求S△AOC;
(3)设直线y=k1x+b与x轴的交点D;在双曲线上是否存在合适的点P,使S△PDO=S△AOC?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)先求出双曲线的解析式,即可求出m的值,再利用A,B的坐标求出直线的解析式.
(2)根据等腰三角形的性质和S△AOE=$\frac{1}{2}$|k|,即可求得.
(3)求得D的坐标,然后根据已知条件得出$\frac{1}{2}$×2×|yP|=3,即可求得P的纵坐标,代入反比例函数解析式即可求得坐标.
解答 解:(1)把A(1,3)代入双曲线y=$\frac{{k}_{2}}{x}$,得3=$\frac{{k}_{2}}{1}$,解得k2=3,
∴双曲线y=$\frac{3}{x}$,
∵B(m,-1),
∴-1=$\frac{3}{m}$,解得,m=-3,
∴B(-3,-1)
把A(1,3)、B(-3,-1)代入y=k1x+b得
$\left\{\begin{array}{l}{3={k}_{1}+b}\\{-1=-3{k}_{1}+b}\end{array}\right.$解得$\left\{\begin{array}{l}{{k}_{1}=1}\\{b=2}\end{array}\right.$
∴直线的解析式为:y=x+2.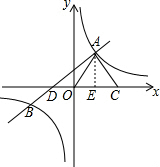
(2)如图,过点A作AE⊥OC于点E,
∵AO=AC,
∴OE=EC,
∵点A在双曲线y=$\frac{3}{x}$图象上,
∴$\frac{1}{2}$OE•AE=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴$\frac{1}{2}$CE•AE=$\frac{3}{2}$,
∴S△AOC=3;
(3)如图,由直线y=x+2可知D(-2,0),
∴OD=2,
∵S△PDO=S△AOC,S△AOC,=3,
∴$\frac{1}{2}$OD•|yP|=3,
∴|yP|=3,
把y=3代入双曲线y=$\frac{3}{x}$,解得x=1,
把y=-3代入双曲线y=$\frac{3}{x}$,解得x=-1,
∴P点的坐标为(1,3)或(-1,-3).
点评 本题考查了待定系数法求反比例函数和一次函数的解析式以及三角形的面积,熟练掌握待定系数法是解题的关键.

| A. | x3与y3 | B. | -xy与yx | C. | 3与3a | D. | 3ab2与3a2b |
| A. | 坐标 | B. | 原点 | C. | 单位长度 | D. | 图形 |
①(+$\frac{3}{5}$)+(-$\frac{4}{5}$);②(-$\frac{6}{7}$)-(-$\frac{5}{6}$);③-4×0;④2×(-3)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 面积相等的两个三角形全等 | B. | 周长相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 成轴对称的两个三角形全等 |
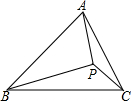 如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.
如图,已知P为△ABC内一点,且∠PAB=∠PCB,∠PBC=∠PAC,求证:P为△ABC的垂心.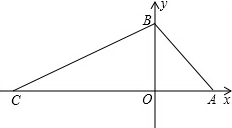 如图,在平面直角坐标系中,O为坐标原点,直线AB与x轴交于点A,与y轴交于点B,且A(4,0),B(0,4),点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).
如图,在平面直角坐标系中,O为坐标原点,直线AB与x轴交于点A,与y轴交于点B,且A(4,0),B(0,4),点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).