题目内容
8.解关于x的方程$\frac{x-a-b}{c}$+$\frac{x-a-c}{b}$+$\frac{x-b-c}{a}$=3(abc≠0).分析 方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:去分母得:ab(x-a-b)+ac(x-a-c)+bc(x-b-c)=3abc,
去括号得:abx-a2b-ab2+acx-a2c-ac2+bcx-b2c-bc2=3abc,
移项合并得:(ab+ac+bc)x=a2b+ab2+a2c+ac2+b2c+bc2+3abc,
解得:x=$\frac{{a}^{2}b+a{b}^{2}+{a}^{2}c+a{c}^{2}+{b}^{2}c+b{c}^{2}}{ab+ac+bc}$.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
19.计算3.8×10-7-3.7×10-7,结果用科学记数法表示为( )
| A. | 0.1×10-7 | B. | 1×10-6 | C. | 0.1×10-8 | D. | 1×10-8 |
16.方程3x-2y=7的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ |
3.将一元二次方程3x2-1=4x化成一般形式为( )
| A. | 3x2+4x=1 | B. | 3x2-4x=1 | C. | 3x2-4x-1=0 | D. | 3x2+4x-1=0 |
20.用配方法解下列方程,其中应在方程左、右两边同时加上4的是( )
| A. | x2-2x=5 | B. | 2x2-4x=5 | C. | x2+4x=5 | D. | 4x2+4x=5 |
17.若关于y的一元二次方程ky2-2y-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | .k<1 | D. | k<1 且k≠0 |
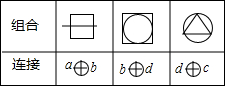 字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形
字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形 的连接方式为a⊕c.
的连接方式为a⊕c.