题目内容
19.已知方程x2-3x+1=0的两根α,β也是方程x6-px2+q=0的根,求p,q的值.分析 方程x2-3x+1=0的两根α,β,得出α+β=3,αβ=1;α,β也是方程x6-px2+q=0的根得出α6-pα2+q=0,β6-pβ2+q=0,进一步恒等变形得出答案即可.
解答 解:∵α,β是方程x2-3x+1=0的两个根,
∴α+β=3,αβ=1,
∵α,β也是方程x6-px2+q=0的根,
∴α6-pα2+q=0,β6-pβ2+q=0,
∴α6-β6-p(α2-β2)=0,
∴p=α4+β4+α2β2=[(α+β)2-2αβ]2-α2β2=48,
∴q=7.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
7.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论中正确的有4个.
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
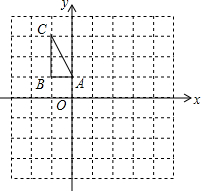 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).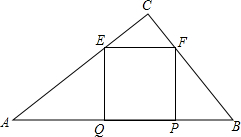 如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.
如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.