题目内容
13.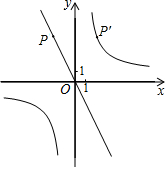 如图,已知直线y=-2x,经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知直线y=-2x,经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.(1)求点P′的坐标;
(2)求反比例函数的解析式,并直接写出当y>1时自变量x的取值范围.
分析 (1)把P的坐标代入直线的解析式,即可求得P的坐标,然后根据关于y轴对称的两个点之间的关系,即可求得P′的坐标;
(2)利用待定系数法即可求得反比例函数的解析式,然后根据反比例函数的增减性即可求得x的范围.
解答 解:(1)将P(-2,a)代入y=-2x得a=-2×(-2)=4,
∴P′(2,4);
(2)将P′(2,4)代入y=$\frac{k}{x}$得4=$\frac{k}{2}$,解得k=8,
∴反比例函数的解析式为y=$\frac{8}{x}$,
∴当y>1时自变量x的取值范围是x<8.
点评 本题考查了待定系数法求函数的解析式,以及反比例函数的性质,容易出现的错误是在求x的范围时忽视x≠0这一条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.写有“盖尾”“武夷山”“三明”“赖店”的四张卡片,从中随机抽取一张,抽到卡片所对应的地区属于莆田市的概率是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
5.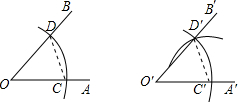 用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
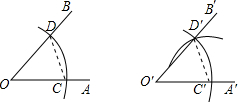 用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
3.小马虎在下面的计算中只做对了一道题,你认为他做对的是( )
| A. | (a+b)2=a2+b2 | B. | (2ab+b)÷b=2a | C. | -2a(b-1)=-2ab-2a | D. | (a+b)(a-b)=a2-b2 |
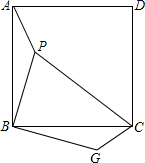 如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.