题目内容
10.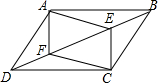 如图,点B,E,F,D在一条直线上,且DE=BF,点A,C在直线BD的两側,且AB=CD,AE=CF.连接AD,AF,CB,CE,则图中的全等三角形共有( )
如图,点B,E,F,D在一条直线上,且DE=BF,点A,C在直线BD的两側,且AB=CD,AE=CF.连接AD,AF,CB,CE,则图中的全等三角形共有( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
分析 先由AE=BF得到AF=BE,则可利用“SSS”判定△ABE≌△CDF,根据全等三角形的性质得∠ABE=∠CDF,加上AB=CD,BF=DE,则可利用“SAS”判定△ABF≌△CDE;△ABD≌△CDB,接着根据全等三角形的性质得AF=CE,AD=CB,∠ADB=∠CBD,然后利用“SSS”判定△AEF≌△CEF,利用“SAS”判定△ADF≌△CBE,△ADE≌△CBF.
解答 解:∵AE=BF,
∴AF=BE,
而AB=CD,AE=CF,
∴可根据“SSS”判定△ABE≌△CDF,
∴∠ABE=∠CDF,
而AB=CD,BF=DE,
∴可根据“SAS”判定△ABF≌△CDE;△ABD≌△CDB,
∴AF=CE,AD=CB,∠ADB=∠CBD,
∴可根据“SSS”判定△AEF≌△CEF,根据“SAS”判定△ADF≌△CBE,△ADE≌△CBF.
故选C.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
20.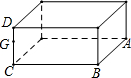 如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
 如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )
如图,地面上有一立方体物块宽AB=4cm,长BC=8cm,CD上的点G距地面的高CG=5cm,地面上一只蚂蚁从A处爬到G处,要爬行的最短路程是( )| A. | 6cm | B. | $4+\sqrt{89}$cm | C. | 13cm | D. | 17cm |
1.已知∠1与∠2互余,∠2与∠3互补,∠1=58°,则∠3=( )
| A. | 58° | B. | 148° | C. | 158° | D. | 32° |
18.下列说法不正确的是( )
| A. | 一个数(不为0)与它的倒数之积是1 | |
| B. | 一个数与它的相反数之和为0 | |
| C. | 两个数的商为-1,这两个数互为相反数 | |
| D. | 两个数的积为1,这两个数互为相反数 |
2.方程-2x=$\frac{1}{2}$的解是( )
| A. | x=-$\frac{1}{4}$ | B. | x=$\frac{1}{4}$ | C. | x=-4 | D. | x=4 |
19.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大是( )


| A. | a | B. | b | C. | c | D. | d |
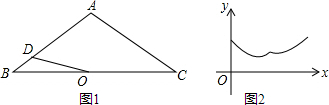
 如图,AC=BD,AC,BD交于点O,要使△ABC≌△DCB,只需添加一个条件,这个条件可以是AB=DC.
如图,AC=BD,AC,BD交于点O,要使△ABC≌△DCB,只需添加一个条件,这个条件可以是AB=DC.