题目内容
19．
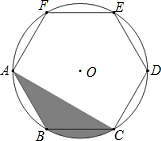如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为6，则阴影部分的面积为（ ）| A． | 12π | B． | 6π | C． | 9π | D． | 18π |
分析 根据图形分析可得求图中阴影部分面积实为求扇形部分面积，将原图阴影部分面积转化为扇形面积求解即可．
解答 解：如图所示：连接BO，CO，OA，
∵正六边形ABCDEF内接于⊙O，
∴△OAB，△OBC都是等边三角形，
∴∠AOB=∠OBC=60°，
∴S△ABC=S△OBC，
∴S阴=S扇形OBC
∴图中阴影部分面积为：S扇形OBC=$\frac{60•π•{6}^{2}}{360}$=6π．
故选B．
点评 此题主要考查了正多边形和圆以及扇形面积求法，得出阴影部分面积=S扇形OBC是解题关键．
练习册系列答案
相关题目
14．
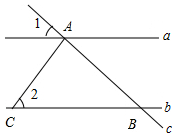如图，直线a∥b，直线c分别与a、b相交于A、B两点，AC⊥AB于点A，交直线b于点C．已知∠1=44°，则∠2的度数是（ ）
如图，直线a∥b，直线c分别与a、b相交于A、B两点，AC⊥AB于点A，交直线b于点C．已知∠1=44°，则∠2的度数是（ ）| A． | 36° | B． | 44° | C． | 46° | D． | 56° |
11．
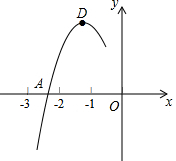抛物线y=ax2+bx+c的顶点D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图，则以下结论：①b2-4ac＜0；②a+b+c＞0；③c-a=2；④方程ax2+bx+c-2=0有两个相等的实数根．
其中正确的结论是（ ）
抛物线y=ax2+bx+c的顶点D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图，则以下结论：①b2-4ac＜0；②a+b+c＞0；③c-a=2；④方程ax2+bx+c-2=0有两个相等的实数根．其中正确的结论是（ ）
| A． | ③④ | B． | ②④ | C． | ②③ | D． | ①④ |
8．
实数a、b在数轴上对应点的位置如图所示，化简$\sqrt{（a-b）^{2}}$-|a+b+1|结果是（ ）
实数a、b在数轴上对应点的位置如图所示，化简$\sqrt{（a-b）^{2}}$-|a+b+1|结果是（ ）| A． | -2b-1 | B． | 2b-1 | C． | 2a-1 | D． | -2a-1 |
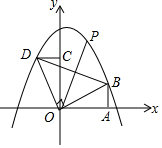如图，Rt△AOB的直角边OA在x轴上，OA=2，AB=1，将Rt△AOB绕点O逆时针旋转90°得到Rt△COD，抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点．