题目内容
9.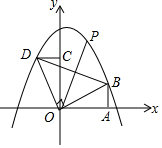 如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.
如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
分析 (1)由旋转性质可得CD=AB=1、OA=OC=2,从而得出点B、D坐标,代入解析式即可得出答案;
(2)由直线OP把△BOD的周长分成相等的两部分且OB=OD,知DQ=BQ,即点Q为BD的中点,从而得出点Q坐标,求得直线OP解析式,代入抛物线解析式可得点P坐标.
解答 解:(1)∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1、OA=OC=2,
则点B(2,1)、D(-1,2),代入解析式,得:
$\left\{\begin{array}{l}{-\frac{10}{3}+2b+c=1}\\{-\frac{5}{6}-b+c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{1}{2}}\\{c=\frac{10}{3}}\end{array}\right.$,
∴二次函数的解析式为y=-$\frac{5}{6}$x2+$\frac{1}{2}$x+$\frac{10}{3}$;
(2)如图,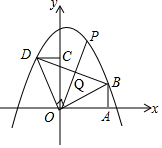
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,
∴点Q坐标为($\frac{1}{2}$,$\frac{3}{2}$),
设直线OP解析式为y=kx,
将点Q坐标代入,得:$\frac{1}{2}$k=$\frac{3}{2}$,
解得:k=3,
∴直线OP的解析式为y=3x,
代入y=-$\frac{5}{6}$x2+$\frac{1}{2}$x+$\frac{10}{3}$,得:-$\frac{5}{6}$x2+$\frac{1}{2}$x+$\frac{10}{3}$=3x,
解得:x=1或x=-4,
当x=1时,y=3,
当x=-4时,y=-12,
∴点P坐标为(1,3)或(-4,-12).
点评 本题主要考查待定系数求函数解析式及二次函数图象上点的坐标特征,熟练掌握待定系数法求函数解析式及根据周长相等得出点Q的坐标是解题的关键.

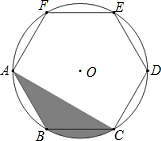 如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )
如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )| A. | 12π | B. | 6π | C. | 9π | D. | 18π |
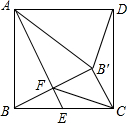 如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交
如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交于点F.下列结论错误的是( )
| A. | AB′=AD | B. | ∠ADB′=75° | ||
| C. | ∠CB′D=135° | D. | △FCB′是等腰直角三角形 |