题目内容
10.在某中学举行的演讲比赛中,八年级5名参赛选手的成绩如下表所示| 选手 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 得分 | 92 | 95 | 91 | 89 | 88 |
(2)计算出这5名选手成绩的方差.
分析 (1)先求出5个选手的得分和,再除以5求平均数即可;
(2)利用方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]计算即可.
解答 解:(1)$\overline{x}$=(95+91+89+88)÷5=91;
(2)S2=$\frac{1}{5}$[(92-91)2+(95-91)2+(91-91)2+(89-91)2+(88-91)2]=6.
点评 本题考查方差的定义和平均数,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.对于任意的正数m、n定义运算※为:m※n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$,计算(3※2)×(8※12)的结果为( )
| A. | 2-4$\sqrt{6}$ | B. | 2 | C. | 2$\sqrt{5}$ | D. | 20 |
18.若$\sqrt{x-3}$是二次根式,则x应满足的条件是( )
| A. | x<3 | B. | x≤3 | C. | x>3 | D. | x≥3 |
5.菱形具有而矩形不具有的性质是( )
| A. | 对角相等 | B. | 四个角相等 | C. | 对角线相等 | D. | 四条边相等 |
15.第六次全国人呢口普查总人口约为1370000000人,该数用科学记数法表示为( )
| A. | 1.37×109 | B. | 13.7×108 | C. | 1.37×1010 | D. | 1.37×108 |
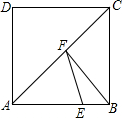 如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( )
如图,在边长为4的长方形ABCD中,E是AB边上一点,且AE=3,点F为对角线AC上的动点,则△BEF周长的最小值为( ) 如图,由A到B的方向是东偏南30°.
如图,由A到B的方向是东偏南30°.