题目内容
7．
如图，在△ABC中，不能判定DE∥CB的条件是（ ）| A． | ∠ADE=∠ABC | B． | ∠DEB=∠CBE | C． | ∠BDE+∠ABC=180° | D． | ∠BDE=∠DEC |
分析 根据平行线的判定定理即可得出正确的选项．
解答 解：A、∵∠ADE=∠ABC，∴DE∥CB，同位角相等，两直线平行，故选项能判定；
B、∵∠DEB=∠CBE，∴DE∥CB，内错角相等两直线平行，故选项能判定；
C、∵∠BDE+∠ABC=180°，∴DE∥CB，同旁内角互补，两直线平行，故选项能判定；
D、∠BDE=∠DEC，不能判定DE∥CB．
故选D．
点评 本题考查了平行线的判定，熟练掌握平行线的判定定理是解题的关键．
练习册系列答案
相关题目
17．
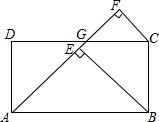如图，在矩形ABCD中，AD=1，AB＞1，AG平分∠BAD，分别过点B、C作BE⊥AG于点E，CF⊥AG于点F，则（AE-GF）的值为（ ）
如图，在矩形ABCD中，AD=1，AB＞1，AG平分∠BAD，分别过点B、C作BE⊥AG于点E，CF⊥AG于点F，则（AE-GF）的值为（ ）| A． | 1 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{2}$ |
15．关于x的方程ax2+bx+c=0，有下列说法：①若a≠0，则方程必是一元二次方程；②若a=0，则方程必是一元一次方程，那么上述说法（ ）
| A． | ①②均正确 | B． | ①②均错 | C． | ①正确，②错误 | D． | ①错误，②正确 |
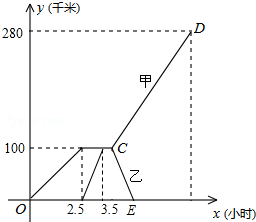已知，A、B两市相距280千米，甲车从A市前往B市运送物资，行驶2.5小时在M地汽车M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计）．乙车到达M地后又经过30分钟修好甲车后原路返回，同时甲车以原速1.5倍的速度前往B市．如图是甲、乙两车距A市的路程y（千米）与甲车行驶时间x（小时）之间的函数图象，结合图象回答下列问题：
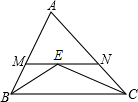如图，在△ABC中，∠ABC和∠ACB的角平分线交于点E，过点E作MN∥BC交AB于点M，交AC于点N．若BM+CN=7，则MN的长为（ ）
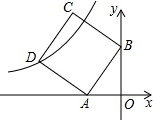在平面直角坐标系中，正方形ABCD如图摆放，点A的坐标为（-1，0），点B的坐标为（0，2），点D在反比例函数y=$\frac{k}{x}$（k＜0）图象上，将正方形沿x轴正方向平移m个单位长度后，点C恰好落在该函数图象上，则m的值是1．
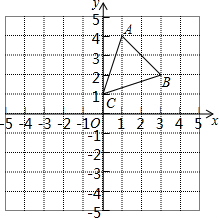如图，三角形ABC是原三角形A1B1C1经过先向右平移3个单位长度，再向上平移1个单位长度得到的．请画出原三角形A1B1C1，并写出点A1、B1、C1的坐标．