题目内容
17. 如图,AB是⊙O的直径,BC是⊙O的切线,弦AD的延长线交直线BC与点C,
如图,AB是⊙O的直径,BC是⊙O的切线,弦AD的延长线交直线BC与点C,(1)若AB=10,∠ACB=60°,求BD的长;
(2)若点E是线段BC的中点,求证:DE是⊙O的切线.
分析 (1)首先根据AB是⊙O的直径,BC是⊙O的切线,可得∠ADB=∠ABC=90°;然后根据∠ACB=60°,求出∠A的度数,即可求出BD的长是多少.
(2)首先连接OD,根据点E是线段BC的中点,判断出∠DBE=∠BDE;然后判断出∠BDE+∠ODB=∠DBE+∠OBD,即∠ODE=∠OBE=90°,再根据DE过半径OD的外端,判断出DE是⊙O的切线即可.
解答 (1)解:∵AB是⊙O的直径,BC是⊙O的切线,
∴∠ADB=∠ABC=90°,
∵∠ACB+∠CBD=∠A+∠ACB,
∴∠A=∠CBD=90°-∠ACB=90°-60°=30°,
∴BD=AB$•sin30°=10×\frac{1}{2}$=5.
(2)证明:如图1,连接OD. ,
,
由(1),可得∠BDC=90°,
∵点E是线段BC的中点,
∴DE=$\frac{1}{2}BC=BE$,
∴∠DBE=∠BDE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠BDE+∠ODB=∠DBE+∠OBD,
即∠ODE=∠OBE=90°,
又∵DE过半径OD的外端,
∴DE是⊙O的切线.
点评 (1)此题主要考查了切线的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.
(2)此题还考查了直角三角形的性质和应用,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列图案中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |




 如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )
如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )



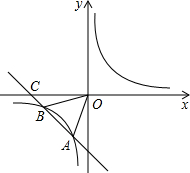 在平面直角坐标系xOy中,O是坐标原点;一次函数y=kx+b(k≠0)图象与反比例函数y=$\frac{m}{x}({m≠0})$的图象交于A(a,2a-1)、B(3a,a).
在平面直角坐标系xOy中,O是坐标原点;一次函数y=kx+b(k≠0)图象与反比例函数y=$\frac{m}{x}({m≠0})$的图象交于A(a,2a-1)、B(3a,a).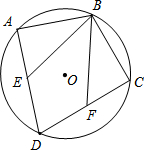 如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.
如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.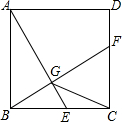 如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)
如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)