题目内容
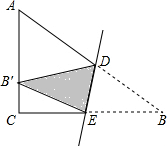 在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.考点:翻折变换(折叠问题)
专题:
分析:设CE=x,表示出BE,再根据翻折的性质可得B′E=BE,然后分两种情况求出B′C,再利用勾股定理列出方程求解即可.
解答:解:设CE=x,则BE=BC-CE=8-x,
∵△BDC沿直线DE折叠B落在点B′处,
∴B′E=BE=8-x,
∵点B′为AC的三等分点,AC=6,
∴B′C=2或B′C=4,
当B′C=2时,在Rt△B′CE中,B′C2+CE2=B′E2,
即22+x2=(8-x)2,
解得x=
,
当B′C=4时,在Rt△B′CE中,B′C2+CE2=B′E2,
即42+x2=(8-x)2,
解得x=3.
综上所述,CE的长度为
或3.
∵△BDC沿直线DE折叠B落在点B′处,
∴B′E=BE=8-x,
∵点B′为AC的三等分点,AC=6,
∴B′C=2或B′C=4,
当B′C=2时,在Rt△B′CE中,B′C2+CE2=B′E2,
即22+x2=(8-x)2,
解得x=
| 15 |
| 2 |
当B′C=4时,在Rt△B′CE中,B′C2+CE2=B′E2,
即42+x2=(8-x)2,
解得x=3.
综上所述,CE的长度为
| 15 |
| 2 |
点评:本题考查了翻折变换的性质,勾股定理的应用,熟记性质并表示出△B′CE的三边的长度,然后利用勾股定理列出方程是解题的关键,要注意分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 由六个相同的正方体搭成的几何体如图,则它的主视图是( )
由六个相同的正方体搭成的几何体如图,则它的主视图是( )A、 |
B、 |
C、 |
D、 |

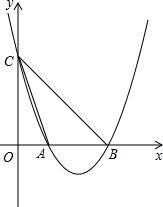 如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点,
如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点, 如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.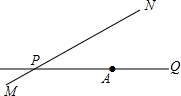 如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行驶时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶.学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行驶时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶.学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?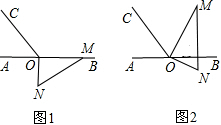 如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方. 如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行
如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵数的树梢,问小鸟至少飞行