题目内容
10．一个不透明的布袋中有4个红球、5个白球、11个黄球，它们除颜色外都相同．（1）求从袋中摸出一个球是红球的概率；
（2）现从袋中取走若干个黄球，并放入相同数量的红球，搅拌均匀后，要使从袋中摸出一个球是红球的概率不小于$\frac{1}{3}$，问至少需取走多少个黄球？
分析 （1）先求出球的总数，再根据概率公式即可得出结论；
（2）设取走x个黄球，则放入x个红球，根据概率公式求解即可．
解答 解：（1）∵袋中有4个红球、5个白球、11个黄球，
∴摸出一个球是红球的概率=$\frac{4}{4+5+11}$=$\frac{1}{5}$；
（2）设取走x个黄球，则放入x个红球，
由题意得，$\frac{4+x}{4+5+11}$≥$\frac{1}{3}$，解得x≥$\frac{8}{3}$，
∵x为整数，
∴x的最小正整数值是3．
答：至少取走3个黄球．
点评 本题考查的是概率公式，熟知随机事件A的概率P（A）=事件A可能出现的结果数与所有可能出现的结果数的商是解答此题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
20．
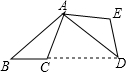如图，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转，得到△ADE，点D恰好落在直线BC上，则旋转角的度数为（ ）
如图，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转，得到△ADE，点D恰好落在直线BC上，则旋转角的度数为（ ）| A． | 70° | B． | 80° | C． | 90° | D． | 100° |
如图，在4×4的方格纸中，每个小正方形边长为1，点O，A，B在方格纸的交点（格点）上，在第四象限内的格点上找一点C，使△ABC的面积为2，则点C的坐标是（1，-1）或（2，-1）．
15．
如图，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③$\frac{AC}{CD}$=$\frac{AB}{BC}$； ④AC2=AD•AB．其中能够单独判定△ABC∽△ACD的条件个数为（ ）
如图，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③$\frac{AC}{CD}$=$\frac{AB}{BC}$； ④AC2=AD•AB．其中能够单独判定△ABC∽△ACD的条件个数为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
19．已知抛物线的表达式为y=2（x+1）2-3，则它的顶点坐标是（ ）
| A． | （1，3） | B． | （1，-3） | C． | （-1，3） | D． | （-1，-3） |