题目内容
12.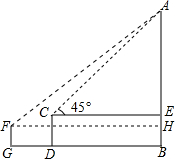 在数学活动课上,小明和小红分别在不同位置测量学校的旗杆高度,如图是他们在测量后绘制的示意图,小明测角仪测得旗杆顶端A的仰角∠ACE=45°,测角仪的高度CD=1.7m,测角仪CD的底部D处与旗杆的底部B处之间的距离DB=8.6cm,小红用同样的方法测得数据∠AFH=40°,FG=1.5cm,GB=10.2cm,点G,D,B在同一条直线上.
在数学活动课上,小明和小红分别在不同位置测量学校的旗杆高度,如图是他们在测量后绘制的示意图,小明测角仪测得旗杆顶端A的仰角∠ACE=45°,测角仪的高度CD=1.7m,测角仪CD的底部D处与旗杆的底部B处之间的距离DB=8.6cm,小红用同样的方法测得数据∠AFH=40°,FG=1.5cm,GB=10.2cm,点G,D,B在同一条直线上.(1)利用小明和小红的测量数据,分别求出他们测量旗杆AB的高度(精确到0.1m);
(2)这两名同学测量旗杆高度的平均值约为10.2m(精确到1m)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
分析 (1)在Rt△ACE中,得到AE=CE=DB=8.6m,在Rt△AFH中,得到AH=FH•tan40°,进而得到旗杆高度;
(2)将两次测量的值相加后求平均数即可.
解答 解:(1)在Rt△ACE中,AE=CE=DB=8.6m,
AB=1.7+8.6=10.3m;
在Rt△AFH中,AH=FH•tan40°=BG•tan40°≈10.2×0.84=8.568m,
AB≈8.568+1.5=10.068m≈10.1m,
(2)这两名同学测量旗杆高度的平均值约为$\frac{10.3+10.1}{2}$=10.2m.
故答案为10.2m.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
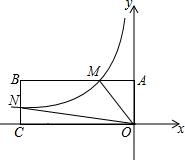 如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).
如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,OC在x轴的负半轴上,OA在y轴的正半轴上,顶点B的坐标为(-6,1).反比例函数y=-$\frac{2}{x}$(x<0)的图象与AB交于点M,与BC交于点N,若点P在y轴上,使S△OMP=S四边形OMBN,则点P的坐标为(0,4)或(0,-4).