题目内容
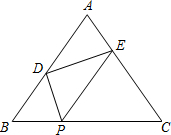如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，BP=2，将一个大小与∠B相等的角的顶点放在P点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E．若△PDE为直角三角形，则BD的长为考点：相似三角形的判定与性质,等腰三角形的性质,勾股定理
专题：分类讨论
分析：如图，作辅助线；求出cos∠B=
；证明△BDP∽△CPE，
=
，而PC=6-2=4，得到BD=4×
；运用分类讨论的数学思想求出
的值，即可解决问题．
| 3 |
| 5 |
| BD |
| PC |
| PD |
| PE |
| PD |
| PE |
| PD |
| PE |
解答：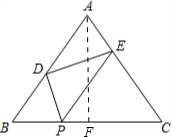
解：如图，过点A作AF⊥BC于点F；
∵AB=AC，
∴∠B=∠C，BF=CF=3；cos∠B=
；
而∠DPE=∠B，
∴∠BDP+∠DPB=∠DPB+∠EPC，
∴∠BDP=∠EPC，
∴△BDP∽△CPE，
∴
=
，而PC=6-2=4，
∴BD=4×
；
若∠PDE=90°，则cos∠DPE=cos∠B=
=
，
∴BD=
；
若∠PED=90°，则cos∠DPE=cos∠B=
=
，
∴BD=
，
故答案为
或
．
解：如图，过点A作AF⊥BC于点F；∵AB=AC，
∴∠B=∠C，BF=CF=3；cos∠B=
| 3 |
| 5 |
而∠DPE=∠B，
∴∠BDP+∠DPB=∠DPB+∠EPC，
∴∠BDP=∠EPC，
∴△BDP∽△CPE，
∴
| BD |
| PC |
| PD |
| PE |
∴BD=4×
| PD |
| PE |
若∠PDE=90°，则cos∠DPE=cos∠B=
| PD |
| PE |
| 3 |
| 5 |
∴BD=
| 12 |
| 5 |
若∠PED=90°，则cos∠DPE=cos∠B=
| PE |
| PD |
| 3 |
| 5 |
∴BD=
| 20 |
| 3 |
故答案为
| 12 |
| 5 |
| 20 |
| 3 |
点评：该题主要考查了等腰三角形的性质、直角三角形的边角关系、相似三角形的判定及其性质等几何问题；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
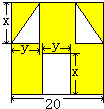“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．关于x的方程3xm-1+2=-3是一元一次方程，则3my+2y=3+m的解是（ ）
A、y=
| ||
| B、y=-3 | ||
| C、y=3 | ||
D、y=
|
如图，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，如果AB：AD=3：5，那么tan∠EFC值是
如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点重合，若AB=2，BC=3，则△FCB′与△B′DG的面积之比为一个等腰三角形的周长为10cm，腰长为xcm，底边长为ycm，则y与x的函数关系式和自变量的取值范围为（ ）
A、y=5-
| ||||
| B、y=10-2x（0＜x＜5） | ||||
C、y=5-
| ||||
D、y=10-2x（
|
若
=
，
=
，则
的值为（ ）
| a |
| b |
| 5 |
| 7 |
| a |
| c |
| 1 |
| 3 |
| a+b |
| b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|