题目内容
若
=
，
=
，则
的值为（ ）
| a |
| b |
| 5 |
| 7 |
| a |
| c |
| 1 |
| 3 |
| a+b |
| b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：比例的性质
专题：
分析：先由
=
，
=
，可得a：b：c=5：7：15，再设a=5k，b=7k，c=15k，然后把a、b、c的值代入代数式进行计算即可得解．
| a |
| b |
| 5 |
| 7 |
| a |
| c |
| 1 |
| 3 |
解答：解：∵
=
，
=
=
，
∴a：b：c=5：7：15，
设a=5k，则b=7k，c=15k，
所以
=
=
=
．
故选B．
| a |
| b |
| 5 |
| 7 |
| a |
| c |
| 1 |
| 3 |
| 5 |
| 15 |
∴a：b：c=5：7：15，
设a=5k，则b=7k，c=15k，
所以
| a+b |
| b+c |
| 5k+7k |
| 7k+15k |
| 12k |
| 22k |
| 6 |
| 11 |
故选B．
点评：本题考查了比例的性质，得出a：b：c=5：7：15，进而利用“设k法”表示出a、b、c是解题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
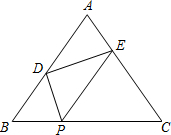如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，BP=2，将一个大小与∠B相等的角的顶点放在P点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E．若△PDE为直角三角形，则BD的长为
如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为在△ABC和△DEF中，给出以下四个条件：①AB=DE；②BC=EF；③AC=DF；④∠A=∠D．从中任意取三个作为已知条件．抽取出来的条件能确定这两个三角形全等的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，△ABC中，∠C=90°，AB=5，BC=3，CA=4，那么sinA等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|