题目内容
14.解不等式(组)(1)-$\frac{1}{2}$(x-3)>4
(2)$\left\{\begin{array}{l}{3x+1<x-3}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1}\end{array}\right.$.
分析 (1)先把不等式两边乘以-2得到x-3<-8,然后把不等式两边加上3即可;
(2)分别解两个不等式得到x<-2和 x≥-5,然后根据大小小大中间找确定原不等式组的解集.
解答 解:(1)x-3<-8,
x<-5;
(2)$\left\{\begin{array}{l}{3x+1<x-3①}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1②}\end{array}\right.$
解不等式(1),得 x<-2,
解不等式(2),得 x≥-5,
所以原不等式组的解集为-5≤x<-2.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在平面直角坐标系中,点P($\sqrt{(-2)^{2}}$,-2x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.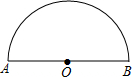 如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )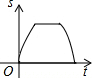



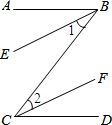 (1)完成下面的推理说明:
(1)完成下面的推理说明: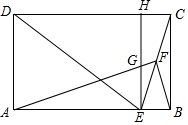 如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
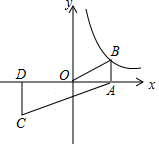 已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.