题目内容
4. 如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.
如图,在矩形ABCD中,对角线AC、BD交于点O,将△ABC沿直线AC翻折,点B落在点B′处,且AB′∥BD,连接B′D.求证:(1)△ABO是等边三角形.
(2)B′D∥AC.
分析 (1)由四边形ABCD是矩形,得到∠BAD=90°,AO=OD,得到∠OAD=∠ADO,根据平行线的性质得到∠B′AD=∠ADB,等量代换得到∠B′AD=∠DAC,根据折叠的性质得到∠BAC=∠CAB′,得到∠DAC=$\frac{1}{2}∠$BAC,求得∠BAC=60°,于是得到结论;
(2)连接B′O,推出B′C垂直平分OD,得到B′O=B′D,根据等腰三角形的性质得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到结论.
解答 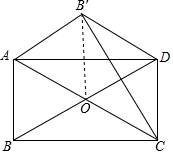 证明:(1)∵四边形ABCD是矩形,
证明:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,AO=OD,
∴∠OAD=∠ADO,
∵AB′∥BD,
∴∠B′AD=∠ADB,
∴∠B′AD=∠DAC,
∵将△ABC沿直线AC翻折,点B落在点B′处,
∴∠BAC=∠CAB′,
∴∠DAC=$\frac{1}{2}∠$BAC,
∴∠BAC=60°,
∵OA=OB,
∴△ABO是等边三角形;
(2)连接B′O,
∵∠COD=∠AOB=60°,∠ACB′=∠ACB=30°,
∴CB′⊥OD,
∵CD=OC,
∴B′C垂直平分OD,
∴B′O=B′D,
∵AO=CO,∠AB′C=90°,
∴B′O=OC,
∴∠OB′C=∠OCB′=30°,
∴∠DB′C=∠OB′C=30°,
∴∠OCB′=∠CB′D,
∴B′D∥AC.
点评 本题考查了翻折变换-折叠问题,矩形的性质,平行线的判定,线段垂直平分线的判定和性质,等边三角形的判定,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
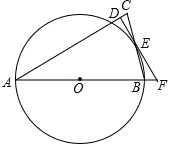 如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.
如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作O的切线交AC于点D,且ED⊥AC.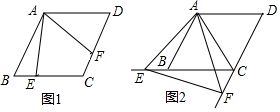
 七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.
七巧板被西方人称为“东方魔板”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图a)的边长为4,则“一帆风顺”(如图b)阴影部分的面积为1.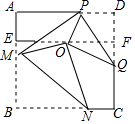 如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.
如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.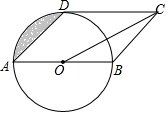 如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.