题目内容
15. 已知二次函数y=-x2+(m-1)x+m.
已知二次函数y=-x2+(m-1)x+m.(1)证明:不论m取何值,该函数图象与x轴总有公共点;
(2)若该函数的图象与y轴交点于(0,3),求出顶点坐标并画出该函数;
(3)在(2)的条件下,观察图象,不等式-x2+(m-1)x+m>3的解集是0<x<2.
分析 (1)令y=0得到关于x的方程,找出相应的a,b及c的值,表示出b2-4ac,整理配方后,根据完全平方式大于等于0,判断出b2-4ac大于等于0,可得出抛物线与x轴总有交点,得证;
(2)由抛物线与y轴交于(0,3),将x=0,y=3代入抛物线解析式,求出m的值,进而确定出抛物线解析式,配方后找出顶点坐标,根据确定出的解析式列出相应的表格,由表格得出7个点的坐标,在平面直角坐标系中描出7个点,然后用平滑的曲线作出抛物线的图象,如图所示;
(3)由图象可得出不等式-x2+(m-1)x+m>3的解集.
解答 (1)证明:令y=0,得到-x2+(m-1)x+m=0,
∵a=-1,b=m-1,c=m,
∴b2-4ac=(m-1)2+4m=(m+1)2,
又(m+1)2≥0,即b2-4ac≥0,
∴方程y=-x2+(m-1)x+m有实数根,
则该函数图象与x轴总有公共点;
(2)解:∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:m=3,
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4);
列表如下:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |
画图如下:
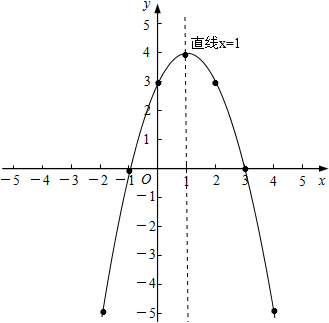
(3)解:由图象可得:不等式-x2+(m-1)x+m>3的解集是0<x<2,
故答案为0<x<2.
点评 此题考查了抛物线与x轴的交点,利用待定系数法确定函数解析式,函数图象的画法,以及二次函数的图象与性质,是一道综合性较强的试题.

练习册系列答案
相关题目
6.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 正三角形 | D. | 圆 |
 直线AB上一点,OM平分∠AOC,ON平分∠BOC,∠BON=28°,则∠BOC=56°,∠BOM=118°,图中互补的角有5对.
直线AB上一点,OM平分∠AOC,ON平分∠BOC,∠BON=28°,则∠BOC=56°,∠BOM=118°,图中互补的角有5对. 如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是160°.
如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是160°. 如图,已知线段AD、BC交于点E,AE=CE,BE=DE.求证:△ABE≌△CDE.
如图,已知线段AD、BC交于点E,AE=CE,BE=DE.求证:△ABE≌△CDE. 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论:
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论: