题目内容
 如图,在△ABC中,AC=BC,CD平分∠ACB交AB于点D,BF平分∠ABC交CD于点F,AB=6,过B、F两点的⊙O交BA于点G,交BC于点E,EB恰为⊙O的直径.
如图,在△ABC中,AC=BC,CD平分∠ACB交AB于点D,BF平分∠ABC交CD于点F,AB=6,过B、F两点的⊙O交BA于点G,交BC于点E,EB恰为⊙O的直径.(1)判断CD和⊙O的位置关系并说明理由;
(2)若cos∠A=
| 1 |
| 3 |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)连接OF,求出OF∥BD,根据等腰三角形性质求出CD⊥AB,推出OF⊥CD,即可得出答案;
(2)解直角三角形求出BC,设半径为r,证△△CFO∽△CDB,得出比例式,代入求出即可.
(2)解直角三角形求出BC,设半径为r,证△△CFO∽△CDB,得出比例式,代入求出即可.
解答:解:(1)CD与⊙O相切,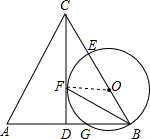
理由如下:连接OF,
∵AC=BC,CD平分∠ACB,
∴AD=BD=3,CD⊥AB,
∴∠BDC=90°,
∵OF=OB,
∴∠OFB=∠OBF,
∵BF平分∠ABC,
∴∠CBF=∠FBD,
∴∠OFB=∠FBD,
∴OF∥DB,
∴∠CFO=∠BDC=90°,
∴CD与⊙O相切;
(2)∵AC=BC,
∴∠A=∠ABC,
∴cos∠ABC=cos∠A=
在Rt△BDC中,cos∠ABC=
=
,
∴BC=9,
∵OF∥DB,
∴△CFO∽△CDB,
设⊙O的半径是r,则
=
,
∴r=
,
即⊙O的半径是
.

理由如下:连接OF,
∵AC=BC,CD平分∠ACB,
∴AD=BD=3,CD⊥AB,
∴∠BDC=90°,
∵OF=OB,
∴∠OFB=∠OBF,
∵BF平分∠ABC,
∴∠CBF=∠FBD,
∴∠OFB=∠FBD,
∴OF∥DB,
∴∠CFO=∠BDC=90°,
∴CD与⊙O相切;
(2)∵AC=BC,
∴∠A=∠ABC,
∴cos∠ABC=cos∠A=
| 1 |
| 3 |
在Rt△BDC中,cos∠ABC=
| 3 |
| BC |
| 1 |
| 3 |
∴BC=9,
∵OF∥DB,
∴△CFO∽△CDB,
设⊙O的半径是r,则
| 9-r |
| 9 |
| r |
| 3 |
∴r=
| 9 |
| 4 |
即⊙O的半径是
| 9 |
| 4 |
点评:本题考查了切线的判定,相似三角形的性质和判定,平行线的性质和判定,等腰三角形的性质的应用,主要考查学生的推理能力,题目比较典型,难度适中.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
若(x-
)2+
=0,则
的值为( )
| 1 |
| 3 |
| 3y-4 |
| xy |
A、
| ||
B、±
| ||
C、±
| ||
D、
|
已知
+
=2
,则a的值是( )
| 2a-3 |
| 5 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
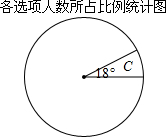 (1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):
(1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):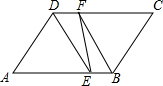 如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.
如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.