题目内容
19.如图1,已知AB=AC,D为∠BAC的平分线上面-点.连接BD,CD;如图2.已知AB=AC,D,E为∠BAC的平分线上面两点.连接BD,CD,BE,CE;
如图3.已知AB=AC,D,E,F为∠BAC的平分线上面三点,连接BD,CD,BE,CE,BF,CF;
…
依此规律,第n个图形中有全等三角形的对数是$\frac{n(n+1)}{2}$.
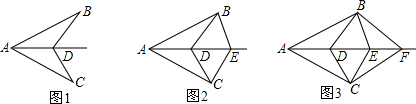
分析 根据条件可得图1中△ABD≌△ACD有1对三角形全等;图2中可证出△ABD≌△ACD,△BDE≌△CDE,△ABE≌△ACE有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n个图形中全等三角形的对数.
解答 解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SAS).
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
在△BDE和△CDE中$\left\{\begin{array}{l}{EB=EC}\\{BD=CD}\\{DE=DE}\end{array}\right.$,
∴△BDE≌△CDE(SSS),
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是$\frac{n(n+1)}{2}$.
故答案为:$\frac{n(n+1)}{2}$.
点评 此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.

练习册系列答案
相关题目
9.下列说法中正确的是( )
| A. | 所有的有理数都可以用数轴上的点来表示 | |
| B. | 数轴上所有的点都表示有理数 | |
| C. | 数轴上找不到既不表示正数也不表示负数的点 | |
| D. | 数轴上表示-a的点一定在原点的左边 |