题目内容
12．在△ABC中，∠C=90°，若a=b，c=m，则a=$\frac{\sqrt{2}}{2}m$，S△ABC=$\frac{1}{4}{m}^{2}$．分析 根据等腰直角三角形的性质解答即可．
解答 解：∵∠C=90°，a=b，c=m，
∴a=b=$\frac{\sqrt{2}}{2}$m，
∴S△ABC=$\frac{1}{2}ab=\frac{1}{2}×\frac{\sqrt{2}}{2}m×\frac{\sqrt{2}}{2}m=\frac{1}{4}{m}^{2}$，
故答案为：$\frac{\sqrt{2}}{2}m$；$\frac{1}{4}{m}^{2}$
点评 此题考查等腰直角三角形的性质，关键是根据等腰直角三角形的性质得出边的关系．
练习册系列答案
阅读快车系列答案
相关题目
2．
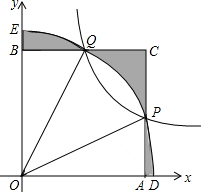如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）
如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）| A． | 3+$\frac{π}{6}$-2$\sqrt{3}$ | B． | 3+$\frac{π}{3}$-2$\sqrt{3}$ | C． | 3+$\frac{π}{6}$-$\sqrt{3}$ | D． | 3+$\frac{π}{3}$-$\sqrt{3}$ |
20．
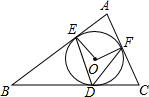如图，⊙O内切于△ABC，切点分别为D，E，F，连接OE，OF，DE，DF，乙组∠A=80°，则∠EDF等于（ ）
如图，⊙O内切于△ABC，切点分别为D，E，F，连接OE，OF，DE，DF，乙组∠A=80°，则∠EDF等于（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 80° |