题目内容
19.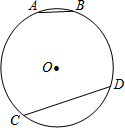 如图,在半径为R的⊙O中,$\widehat{AB}$和$\widehat{CD}$度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).( )
如图,在半径为R的⊙O中,$\widehat{AB}$和$\widehat{CD}$度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).( )| A. | R | B. | $\frac{1}{2}R$ | C. | 2R | D. | 3R |
分析 如解答图,作辅助线,构造三个等腰三角形△OAB,△OCD与△OCE;证明△COE≌△OAB,则有OE=AB;利用等腰三角形性质证明DE=OE,因此CD-AB=CD-DE=CE=R.
解答 解:如图,
连接OA、OB,则△OAB为等腰三角形,顶角为36°,底角为72°;
连接OC、OD,则△OCD为等腰三角形,顶角为108°,底角为36°.
在CD上取一点E,使得CE=OC,连接OE,则△OCE为等腰三角形,顶角为36°,底角为72°.
在△COE与△OAB中,
$\left\{\begin{array}{l}CO=OA=R\\∠OCE=∠AOB=36°\\ CE=OB=R\end{array}\right.$,
∴△COE≌△OAB(SAS),
∴OE=AB.
∵∠EOD=∠OEC-∠ODC=72°-36°=36°,
∴∠EOD=∠ODE,
∴DE=OE,
∴CD-AB=CD-OE=CD-DE=CE=R.
故选:A.
点评 此题考查了圆心角、弧、弦的关系、全等三角形、等腰三角形等知识,解题关键是添加辅助线,构造等腰三角形.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
10.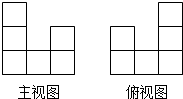 如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
 如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )
如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最多是( )| A. | 11个 | B. | 12个 | C. | 13个 | D. | 14个 |
4.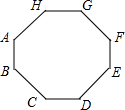 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )| A. | 7 | B. | 8 | C. | 9 | D. | 14$\sqrt{2}$ |
11.若M(-$\frac{1}{2}$,y1)、N(-$\frac{1}{4}$,y2)、P($\frac{1}{2}$,y3)三点都在函数y=-$\frac{1}{x}$的图象上,则y1、y2、y3的大小关系为( )
| A. | y2>y3>y1 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
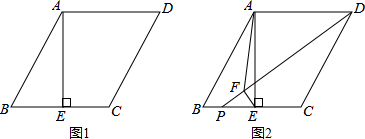
 已知ABCD为正方形,△AEF为等边三角形,求证:
已知ABCD为正方形,△AEF为等边三角形,求证: