��Ŀ����
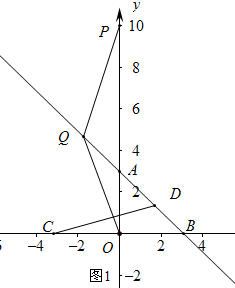
17����ͼ1����ƽ��ֱ������ϵ�У���֪��A��B������ֱ�Ϊ��0��3������3��0����1����ֱ��AB�Ľ���ʽ��
��2����ͼ2����C�ǵ�B����y��ĶԳƵ㣬��D��AB���е㣬��PΪy������ԭ���������᷽���˶���һ���㣬�˶��ٶ�Ϊ2����λ����/s�����P�˶���ʱ��Ϊts����QΪ����BA��һ�㣬��t=5ʱ��$\frac{{S}_{��PQO}}{{S}_{��CDB}}$=$\frac{5}{3}$�����Q�����ꣻ
��3����ͼ3���ڣ�2���������£�����PDCΪ����ֱ��������ʱ����t��ֵ��

���� ��1�����ݴ���ϵ��������ȷ��ֱ��AB�Ľ���ʽ��
��2���������D�����꣬��Q��m��n�������������ε������ʽ����$\frac{{S}_{��PQO}}{{S}_{��CDB}}$=$\frac{5}{3}$�����ɽ�����⣮
��3����DM��OB��DN��OP�����á�DNP�ա�DMC�����PN���ɣ�
���  �⣺��1����ֱ��ABΪy=kx+b��
�⣺��1����ֱ��ABΪy=kx+b��
��A��0��3����B��3��0���ֱ�����$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=-x+3��
��2����ͼ1����Q��m��n��
��P��0��10����A��0��3����B��3��0����AD=DB
��D��$\frac{3}{2}$��$\frac{3}{2}$����
��$\frac{{S}_{��PQO}}{{S}_{��CDB}}=\frac{5}{3}$
��$\frac{\frac{1}{2}��10��|m|}{\frac{1}{2}��6��\frac{3}{2}}=\frac{5}{3}$��
��m=$��\frac{3}{2}$��
�ߵ�Q��ֱ��AB�ϣ���m=$\frac{3}{2}$ʱ��n=$\frac{3}{2}$��m=-$\frac{3}{2}$ʱ��n=$\frac{9}{2}$��
��Q��$\frac{3}{2}$��$\frac{3}{2}$����-$\frac{3}{2}$��$\frac{9}{2}$����
��3��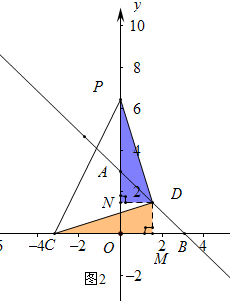 ��ͼ2����DM��BO��DN��OP����ֱ�ΪM��N��
��ͼ2����DM��BO��DN��OP����ֱ�ΪM��N��
�ߡ�PDC�ǵ���ֱ�������Σ�
��DP=DC��
�ߵ�D���꣨$\frac{3}{2}$��$\frac{3}{2}$����
��DM=DN=$\frac{3}{2}$��
��RT��DNP��RT��DMC��
$\left\{\begin{array}{l}{DP=DC}\\{DN=DM}\end{array}\right.$��
��RT��DNP��RT��DMC��
��PN=CM��
��CM=$\frac{9}{2}$��ON=$\frac{3}{2}$��
PN=$\frac{9}{2}$��PO=6��
��t=$\frac{6}{2}$=3��
���� ���⿼�����ô���ϵ������һ�κ����Ľ���ʽ�������ε������ʽ��ȫ�������ε��ж������ʡ����������ε����ʡ���������Ĺ�ϵ��֪ʶ��ͨ���������߹���ȫ���������ǽ����3�ʵĹؼ���

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д� ��ͼ���й��������̵�һ���֣���
��ͼ���й��������̵�һ���֣��� λ�ڵ㣨1��-1������
λ�ڵ㣨1��-1������ λ�ڵ㣨������
λ�ڵ㣨������| A�� | ��3��-2�� | B�� | ��2��-3�� | C�� | ��-2��3�� | D�� | ��-3��2�� |
 ��ͼ����֪��A��˫����$y=\frac{2}{x}$�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ��������Rt��ABC����C�ڵ������ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ���ڵ������ޣ���˫����$y=\frac{k}{x}$ʼ�վ�����C����k��ֵΪ-2��
��ͼ����֪��A��˫����$y=\frac{2}{x}$�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ��������Rt��ABC����C�ڵ������ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ���ڵ������ޣ���˫����$y=\frac{k}{x}$ʼ�վ�����C����k��ֵΪ-2�� ��ͼ��������y=ax2+bx+3��x���ཻ�ڵ�A��-3��0����B��-1��0������y���ཻ�ڵ�C����O1Ϊ��ABC�����Բ��������������һ��D��
��ͼ��������y=ax2+bx+3��x���ཻ�ڵ�A��-3��0����B��-1��0������y���ཻ�ڵ�C����O1Ϊ��ABC�����Բ��������������һ��D�� ��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4��������ABC���ŵ�B˳ʱ����ת90���õ���A1BC1������ͼ�л�����A1BC1��������߶�BC��ת��������ɨ�����������������У�
��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4��������ABC���ŵ�B˳ʱ����ת90���õ���A1BC1������ͼ�л�����A1BC1��������߶�BC��ת��������ɨ�����������������У� ��ͼ����AOB=���㣬��P�ǡ�AOB������һ�㣬OP=6cm����M�͵�N�ֱ�������OA������OB�ϵĶ��㣬����PMN�ܳ�����Сֵ��6cm�������ֵ�ǣ�������
��ͼ����AOB=���㣬��P�ǡ�AOB������һ�㣬OP=6cm����M�͵�N�ֱ�������OA������OB�ϵĶ��㣬����PMN�ܳ�����Сֵ��6cm�������ֵ�ǣ������� ��֪��ͬ��Բ�У���Բ����AB��СԲ��T����T��ֱ�߽���Բ��C��D����СԲ��E��
��֪��ͬ��Բ�У���Բ����AB��СԲ��T����T��ֱ�߽���Բ��C��D����СԲ��E�� ��ͼ���ı���ABCD��һ�ų�����ֽƬ��AD=4���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ���ͼ�еĵ�A�䣩���ۺ۽�AB�ڵ�E����ʱ��á�ADE=15����BE=2$\sqrt{3}$-2��
��ͼ���ı���ABCD��һ�ų�����ֽƬ��AD=4���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ���ͼ�еĵ�A�䣩���ۺ۽�AB�ڵ�E����ʱ��á�ADE=15����BE=2$\sqrt{3}$-2��