题目内容
5. 如图,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
如图,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.(1)求抛物线的解析式;
(2)求⊙O1的半径.
分析 (1)利用待定系数法求出抛物线的解析式;
(2)如图所示,由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度.
解答 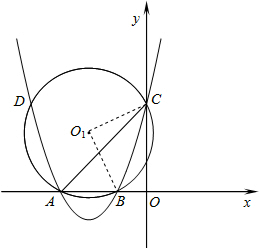 解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),
∴$\left\{\begin{array}{l}{9a-3b+3=0}\\{a-b+3=0}\end{array}\right.$,
解得a=1,b=4,
∴抛物线的解析式为:y=x2+4x+3;
(2)由(1)知,抛物线解析式为:y=x2+4x+3,
∵令x=0,得y=3,
∴C(0,3),
∴OC=OA=3,则△AOC为等腰直角三角形,
∴∠CAB=45°,
在Rt△BOC中,由勾股定理得:BC=$\sqrt{{1}^{1}+{3}^{2}}$=$\sqrt{10}$,
如图1所示,连接O1B、O1B,
由圆周角定理得:∠BO1C=2∠BAC=90°,
∴△BO1C为等腰直角三角形,
∴⊙O1的半径O1B=$\frac{\sqrt{2}}{2}$BC=$\sqrt{5}$.
点评 本题综合考查了二次函数的图象与性质、待定系数法求函数解析式、圆的性质、等腰直角三角形的性质、勾股定理、正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 已知,如图是由八个全等的直角三角形拼接而成的图形.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1,S2,S3,若正方形EFGH的边长为2,则S1+S2+S3的值为( )
已知,如图是由八个全等的直角三角形拼接而成的图形.记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1,S2,S3,若正方形EFGH的边长为2,则S1+S2+S3的值为( ) 已知直线l1:y=-$\frac{3}{4}x+3$与直线l2:y=kx-$\frac{16}{3}$交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
已知直线l1:y=-$\frac{3}{4}x+3$与直线l2:y=kx-$\frac{16}{3}$交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C. 如图是某校的平面示意图,如果分别用(3,-1)、(-3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为(0,-2).
如图是某校的平面示意图,如果分别用(3,-1)、(-3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为(0,-2).
