题目内容
20.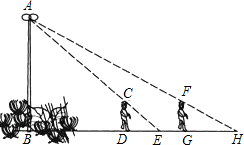 一天晚上,小丽和小华在广场上散步,看见广场上有一路灯杆AB(如图),爱动脑筋的小丽和小华想利用投影知识来测量路灯杆AB的高度.请看下面的一段对话:
一天晚上,小丽和小华在广场上散步,看见广场上有一路灯杆AB(如图),爱动脑筋的小丽和小华想利用投影知识来测量路灯杆AB的高度.请看下面的一段对话:小丽:小华,你站在点D处,我量得你的影长DE是4m;然后你再沿着直线BK走到点G处,又量得DG为6m,此时你的影长GH也是6m;
小华:昨天体检时,医生说我的身高是1.6m,
请你根据她们的对话及示意图,求出该杆AB的高度.
分析 根据AB⊥BH,CD⊥BH,FG⊥BH,可得:△ABE∽△CDE,则有$\frac{CD}{AB}=\frac{DE}{DE+BD}$和$\frac{FG}{AB}$=$\frac{HG}{HG+DG+BD}$,而$\frac{CD}{AB}$=$\frac{FG}{AB}$,即$\frac{DE}{DE+BD}$=$\frac{HG}{HG+DG+BD}$,从而求出BD的长,再代入前面任意一个等式中,即可求出AB.
解答 解:根据题意得:AB⊥BH,CD⊥BH,FG⊥BH,
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,
∴CD∥AB,
可证得:
△ABE∽△CDE,
∴$\frac{CD}{AB}=\frac{DE}{DE+BD}$①,
同理:$\frac{FG}{AB}$=$\frac{HG}{HG+DG+BD}$②,
又CD=FG=1.6m,
由①、②可得:$\frac{DE}{DE+BD}$=$\frac{HG}{HG+DG+BD}$,
即$\frac{4}{4+BD}$=$\frac{6}{12+BD}$,
解得:BD=12m,
将BD=12代入①得:AB=6.4m,
答:该杆AB的高度为6.4米.
点评 本题考查了中心投影及相似三角形的应用,解这道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形中,利用相似比列出方程即可求出.

练习册系列答案
相关题目
8.在2,$\frac{1}{2}$,0,-2四个数中,最大的数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
10.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | |-$\frac{1}{7}$| | D. | $\sqrt{2}$ |
 如图,其中邻补角共有3对.
如图,其中邻补角共有3对.
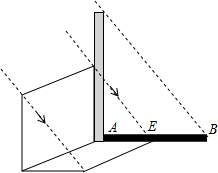 如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图.
如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图. 如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.
如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.