题目内容
13.关于x的一元二次方程 kx2+2x-1=0有两个不相等实数根,则k 的取值范围是( )| A. | k>-1 | B. | k≥-1 | C. | k≠0 | D. | k>-1且k≠0 |
分析 根据一元二次方程的定义和判别式的意义得到k≠0且△=22-4k×(-1)>0,然后解两个不等式求出它们的公共部分即可.
解答 解:根据题意得k≠0且△=22-4k×(-1)>0,
所以k>-1且k≠0.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
4.与-3的差为0的数是( )
| A. | 3 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
1.下列关于矩形的说法,正确的是( )
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相平分的四边形是矩形 | ||
| C. | 矩形的对角线相等且互相平分 | D. | 矩形的对角线互相垂直且平分 |
18.下列三条线段不能构成三角形的三边的是( )
| A. | 3cm,4cm,5cm | B. | 5cm,6cm,11cm | C. | 5cm,6cm,10cm | D. | 2cm,3cm,4cm |
5. 如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )
 如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
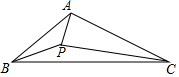 在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB.
在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB. 如图,已知∠B=∠C,点B,A,D在同一直线上,AE平分∠DAC,说明AE∥BC的理由.
如图,已知∠B=∠C,点B,A,D在同一直线上,AE平分∠DAC,说明AE∥BC的理由.