题目内容
8.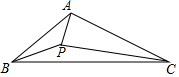 在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB.
在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB.
分析 在BA延长线上取一点D,使BD=BC,连DP,DC.根据BP平分∠ABC,可知C点与点D关于BP对称,得到PD=PC,根据等腰三角形的性质得到∠PDC=∠PCD,∠BDC=∠BCD,等量代换得到∠ADP=∠BCP,根据外角的性质得到∠DPC=2(∠PBC+∠PCB)=60°,推出△PDC是正三角形,得到PC=DC,根据等腰三角形的判定得到AC=PC,根据三角形的内角和即可得到结论.
解答  解:在BA延长线上取一点D,使BD=BC,连DP,DC.
解:在BA延长线上取一点D,使BD=BC,连DP,DC.
∵BP平分∠ABC,可知C点与点D关于BP对称,
∴PD=PC,
∴∠PDC=∠PCD,
∵BD=BC,
∴∠BDC=∠BCD,
∴∠ADP=∠BCP,
∵∠DPC=2(∠PBC+∠PCB)=60°,
∴△PDC是正三角形,
∴PC=DC,
在△ACD中,
∵∠ADC=70°=∠BAC,∴AC=DC,∴AC=PC,
在△PCA中,
∵∠PCA=20°,
∴∠PAC=80°.
∴∠PAB=∠BAC-∠PCA=110°-80°=30°.
点评 本题考查了三角形的内角和,等腰三角形的判定和性质,轴对称的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
19. 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )| A. | 50 | B. | 58 | C. | 68 | D. | 70 |
16.把多项式x2+ax+b分解因式,得(x+1)(x-3),则a,b的值分别是( )
| A. | a=-2,b=-3 | B. | a=2,b=3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
3.±2是4的( )
| A. | 平方根 | B. | 算术平方根 | C. | 绝对值 | D. | 相反数 |
13.关于x的一元二次方程 kx2+2x-1=0有两个不相等实数根,则k 的取值范围是( )
| A. | k>-1 | B. | k≥-1 | C. | k≠0 | D. | k>-1且k≠0 |
20.平行四边形、矩形、正方形之间的关系是( )
| A. |  | B. |  | C. |  | D. |  |
18. 如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )
如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )
 如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )
如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )| A. | ∠BOF | B. | ∠DOF | C. | ∠AOE | D. | ∠DOE |
 如图,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b<4的解集为-2≤x<0.
如图,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b<4的解集为-2≤x<0.