题目内容
13.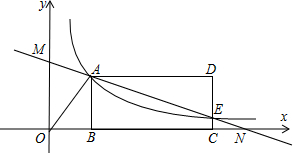 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.(1)求k的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{k}{x}$(x>0)的图象恰好经过DC上一点E,且DE:EC=3:1,求直线AE的函数表达式;
(3)若直线AE与x轴交于点,N,与y轴交于点M,请你探索线段AM与线段NE的大小关系,写出你的结论并说明理由.
分析 (1)在RtOAB中,由三角函数的定义可求得AB的长,则可求得A点坐标,代入反比例函数解析式可求得k的值;
(2)可先求得E点坐标,由A、E的坐标,利用待定系数法可求得直线AE的函数表达式;
(3)延长DA交y轴于点F,由点的坐标,在RtAMF中和Rt△CEN中,利用勾股定理可分别求得AM和NE,可得出结论.
解答 解:
(1)∵在Rt△OAB中,OB=3,tan∠AOB=$\frac{4}{3}$,
∴$\frac{AB}{OB}=\frac{4}{3}$,
∴AB=4,
∴A点的坐标为(3,4),
∴k=xy=12;
(2)∵DC由AB平移得到,DE:EC=3:1,
∴点E的纵坐标为1,
又∵点E在双曲线y=$\frac{12}{x}$上,
∴点E的坐标为(12,1 ),
设直线AE的函数表达式为y=kx+b,则$\left\{\begin{array}{l}4=3k+b\\ 1=12k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{1}{3}\\ b=5\end{array}\right.$,
∴直线AE的函数表达式为 y=-$\frac{1}{3}$x+5;
(3)结论:AM=NE.
理由:在表达式y=-$\frac{1}{3}$x+5中,令y=0可得x=15,令x=0可得y=5
∴点M(0,5),N(15,0 ).
延长DA交y轴于点F,则AF⊥OM,且AF=3,OF=4,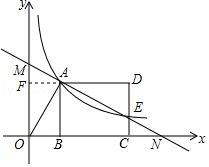
∴MF=OM-OF=1,
∴由勾股定理得AM=$\sqrt{A{F^2}+M{F^2}}=\sqrt{{3^2}+{1^2}}=\sqrt{10}$,
∵CN=15-12=3,EC=1,
∴根据勾股定理可得EN=$\sqrt{C{N^2}+C{E^2}}=\sqrt{{3^2}+{1^2}}={\sqrt{10}^{\;}}$,
∴AM=NE.
点评 本题为反比例函数的综合应用,涉及待定系数法、三角函数的定义、勾股定理等知识.在(1)中求得A点坐标是解题的关键,注意利用三角函数的定义,在(2)中求得E点坐标是解题的关键,在(3)中利用勾股定理分别求得AM和NE的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.

| A. | x2+4 | B. | x2+2 | C. | x2+4x+4 | D. | 2x+4 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 旅游人数(万) | 1.5 | 2.2 | 2.2 | 3.8 | 1.5 | 2.2 | 0.6 |
| A. | 2和2.2 | B. | 2和2 | C. | 1.5和2.2 | D. | 2.2和3.8 |
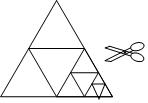 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,第n此操作后,三角形共有(3n+1)个,若要得到100个小三角形,则需要操作的次数是33.
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,第n此操作后,三角形共有(3n+1)个,若要得到100个小三角形,则需要操作的次数是33.