题目内容
14. 如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
分析 (1)使用量角器量出∠AOC,再用直角三角尺画它的平分线,使用直角三角尺画FG⊥AB于G;
(2)根据垂线段最短确定OF和OG的大小;
(3)先利用邻补角计算出∠AOC=180°-∠BOC=140°,再根据角平分线定义得∠AOD=$\frac{1}{2}$∠AOC=70°,然后利用互余计算∠DOE的度数.
解答 解:(1)如图,OD、FG为所画;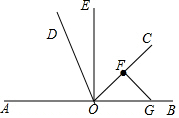
(2)OF<OG.
理由:直线外一点与直线上各点的连线中,垂线段最短;
(3)∠AOC=180°-∠BOC=180°-40°=140°,
∵OD是∠AOC的平分线,
∴∠AOD=$\frac{1}{2}$∠AOC=70°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOE-∠AOD=20°.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
4.下列式子正确的( )
| A. | x-(y-z)=x-y-z | B. | -a+b+c+d=-(a-b)-(-c-d) | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
5.如果a、b是两个不相等的实数,且满足a2-a=2,b2-b=2,那么代数式2a2+ab+2b-2015的值为( )
| A. | 2011 | B. | -2011 | C. | 2015 | D. | -2015 |
3.已知:y-2x=5,则5(y-2x)-3(2x-y)-60的值为( )
| A. | 80 | B. | 40 | C. | -20 | D. | -10 |
 如图,小明做实验时发现,当三角板中30°角的顶点A在⊙O上移动,三角板的两边与⊙O相交于点P、Q时,$\widehat{PQ}$的长度不变.若⊙O的半径为9,则$\widehat{PQ}$的长等于3π.
如图,小明做实验时发现,当三角板中30°角的顶点A在⊙O上移动,三角板的两边与⊙O相交于点P、Q时,$\widehat{PQ}$的长度不变.若⊙O的半径为9,则$\widehat{PQ}$的长等于3π. 如图,数轴上的有理数a,b满足|3a-b|-|a+2b|=|a|,则$\frac{a}{b}$=-$\frac{1}{3}$.
如图,数轴上的有理数a,b满足|3a-b|-|a+2b|=|a|,则$\frac{a}{b}$=-$\frac{1}{3}$. 如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.
如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.