题目内容
12．
如图，AB∥CD，AP，CP分别平分∠BAC和∠ACD，PE⊥AC于点E，且PE=2cm，则AB与CD之间的距离是4cm．
分析 过点P作PM⊥AB于M，作PN⊥CD于N，根据角平分线上的点到角的两边的距离相等可得PM=PE=PN，再根据平行线间的距离的定义解答即可．
解答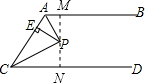 
解：如图，过点P作PM⊥AB于M，作PN⊥CD于N，
∵AP、CP分别平分∠BAC和∠ACD，PE⊥AC，
∴PM=PE=PN=2cm，
∵AB∥CD，PM⊥AB，
∴PM⊥CD，
∵PN⊥CD，
∴M、P、N三点共线，
∴AB与CD之间的距离=PM+PN=4cm．
故答案为4．
点评 本题考查了角平分线上的点到角的两边的距离相等的性质，两平行线间的距离，作辅助线并熟记性质是解题的关键．
练习册系列答案
相关题目
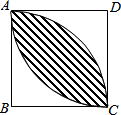如图所示，若正方形边长为a，则阴影部分的面积为（$\frac{1}{2}$π-1）a2．
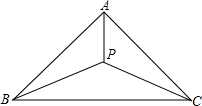三角形ABC中，∠ABC和∠ACB的角平分线相交于点P，连接AP，若∠BPC=130°，则∠BAP=40°．