题目内容
7．若二次函数y=kx2+（k+2）x+5，对于任意负实数k，当x＜m时，y随x的增大而增大，则m的最大整数值为（ ）| A． | 2 | B． | -2 | C． | -1 | D． | 0 |
分析 k＜0，函数y=kx2+（k+2）x+5开口向下，再求出对称轴为：x=-$\frac{k+2}{2k}$=-$\frac{1}{2}$-$\frac{1}{k}$＞-$\frac{1}{2}$，根据x＜m时，y随x的增大而增大，利用二次函数的增减性即可求出m的最大整数值是-1．
解答 解：对于任意负实数k，函数y=kx2+（k+2）x+5的图象是开口向下的抛物线，
对称轴为：x=-$\frac{k+2}{2k}$=-$\frac{1}{2}$-$\frac{1}{k}$＞-$\frac{1}{2}$，
∵当x＜m时，y随x的增大而增大，
∴m的最大整数值是-1．
故选C．
点评 本题考查了二次函数的性质．掌握二次函数的增减性是解题的关键．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
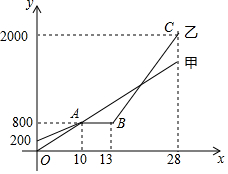甲、乙相约去离家2000m的公园晨练，甲先出发一直匀速前行，乙后出发，如图是甲和乙所走的路程s（m）与时间t（min）的函数图象．
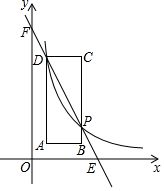如图，矩形ABCD中，点A（1，1）、B（3，1），C（3，6），反比例函数y=$\frac{m}{x}$（x＞0）的图象经过点D，且与BC交于点P．
16．在平面直角坐标系中，点A、B的坐标分别为（2，0），（4，0），点C的坐标为（m，$\sqrt{3}$m）（m为非负数），则CA+CB的最小值是（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 2$\sqrt{7}$ |
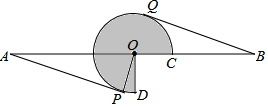如图，AB=16，O为AB中点，点C在线段OB上（不与点O，B重合），将OC绕点O逆时针旋转270°后得到扇形COD，AP，BQ分别切优弧$\widehat{CD}$于点P，Q，且点P，Q在AB异侧，连接OP．