题目内容
5.在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
分析 (1)由在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两次取出的数字的和等于0的情况,再利用概率公式即可求得答案.
解答 解:(1)∵在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别,
∴P(取出负数)=$\frac{1}{3}$;
(2)列表如下:
| -1 | 1 | 2 | |
| -1 | -2 | 0 | 1 |
| 1 | 0 | 2 | 3 |
| 2 | 1 | 3 | 4 |
∴P(和等于0)=$\frac{2}{9}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.在平行四边形、等腰三角形、矩形、菱形四个图形中,既是中心对称图形又是轴对称图形的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.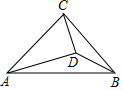 如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
 如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
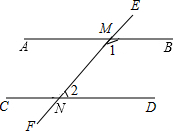 如图,直线AB与直线EF相交于点M,直线CD与直线EF相交于点N;∠1是它的补角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD吗?为什么?
如图,直线AB与直线EF相交于点M,直线CD与直线EF相交于点N;∠1是它的补角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD吗?为什么? 已知:∠AOB(如图所示)
已知:∠AOB(如图所示)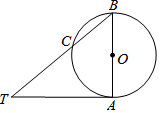 如图,AB是⊙O的直径,TA切⊙O与点A,连接TB交⊙O于点C,∠BTA=40°,点M是圆上异于B、C的一个动点,则∠BMC的度数等于40°或140°.
如图,AB是⊙O的直径,TA切⊙O与点A,连接TB交⊙O于点C,∠BTA=40°,点M是圆上异于B、C的一个动点,则∠BMC的度数等于40°或140°.