题目内容
17.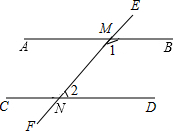 如图,直线AB与直线EF相交于点M,直线CD与直线EF相交于点N;∠1是它的补角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD吗?为什么?
如图,直线AB与直线EF相交于点M,直线CD与直线EF相交于点N;∠1是它的补角的2倍,∠2的余角是∠2的$\frac{1}{2}$,那么AB∥CD吗?为什么?
分析 根据补角定义可得2∠1=180°-∠1,再根据余角定义可得$\frac{1}{2}$∠2=90°-∠2,分别计算出∠1和∠2的度数,再根据同旁内角互补,两直线平行可得AB∥CD.
解答 解:∵∠1是它的补角的2倍,
∴2∠1=180°-∠1,
∠1=120°,
∵∠2的余角是∠2的$\frac{1}{2}$,
∴$\frac{1}{2}$∠2=90°-∠2,
解得:∠2=60°,
∴∠1+∠2=180°,
∴AB∥CD.
点评 此题主要考查了平行线的判定,关键是掌握余角和补角定义,掌握同旁内角互补,两直线平行.

练习册系列答案
相关题目
8. 如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
 如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
2.下列说法中错误的有( )
①若两数的差是正数,则这两个数都是正数 ②任何数的绝对值都不是负数
③零减去任何一个有理数,其差是该数的相反数 ④倒数等于本身的数是1
⑤若两数和为正,则这两个数都是正数.
①若两数的差是正数,则这两个数都是正数 ②任何数的绝对值都不是负数
③零减去任何一个有理数,其差是该数的相反数 ④倒数等于本身的数是1
⑤若两数和为正,则这两个数都是正数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.若x,y为实数,且|x+1|+$\sqrt{y-1}$=0,则xy的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
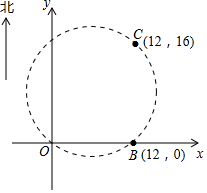 在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.
在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.