题目内容
15.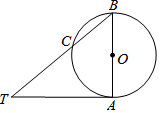 如图,AB是⊙O的直径,TA切⊙O与点A,连接TB交⊙O于点C,∠BTA=40°,点M是圆上异于B、C的一个动点,则∠BMC的度数等于40°或140°.
如图,AB是⊙O的直径,TA切⊙O与点A,连接TB交⊙O于点C,∠BTA=40°,点M是圆上异于B、C的一个动点,则∠BMC的度数等于40°或140°.
分析 先根据切线的性质求出∠BAT的度数,再根据三角形内角和定理求出∠B的度数,由等腰三角形的性质求得∠BOC的度数,由圆周角定理即可解答.
解答 解:∵TA切⊙O于点A,
∴AT⊥AB,
∵∠BTA=40°,
∴∠B=90°-40°=50°,
∵OB=OC,
∴∠OCB=∠B=50°,
∴∠BOC=80°,
∵∠BMC=$\frac{1}{2}$×80°=40°或∠BMC=$\frac{1}{2}$×(360-°80°)=140°.
故答案是:40°或140°.
点评 本题考查了切线的性质,解答此题的关键是熟知切线的性质、三角形内角和定理及圆周角定理,有一定的综合性.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6.若x,y为实数,且|x+1|+$\sqrt{y-1}$=0,则xy的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
5.关于x的一元二次方程ax2+bx+c=0(a≠0)的两根如果互为倒数,那么( )
| A. | a=b | B. | b=c | C. | a=c | D. | a=b=c |
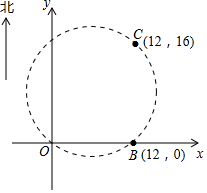 在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.
在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.