题目内容
14.计算:$\sqrt{12}$+$\sqrt{16}$×$\sqrt{\frac{1}{8}}$-2sin45°+|2-$\sqrt{3}$|分析 根据特殊角的三角函数值和二次根式的乘法法则运算,然后去绝对值后合并即可.
解答 解:原式=2$\sqrt{3}$+$\sqrt{16×\frac{1}{8}}$-2×$\frac{\sqrt{2}}{2}$+2-$\sqrt{3}$
=2$\sqrt{3}$+$\sqrt{2}$-$\sqrt{2}$+2-$\sqrt{3}$
=$\sqrt{3}$+2.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
5.下列计算正确的是( )
| A. | 23=6 | B. | -32=9 | C. | (-1)2=1 | D. | 2÷6×$\frac{1}{3}$=1 |
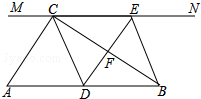 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为E,连结CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为E,连结CD、BE.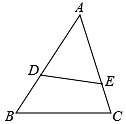 如图,△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是10,则△ADE的面积是8.
如图,△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是10,则△ADE的面积是8.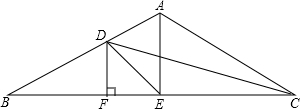 在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC=30°.
在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC=30°.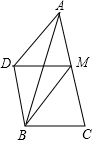 如图在△ABC中,∠BAC=30°,AB=AC=6,M为AC边上一动点(不与A,C重合),以MA、MB为一组邻边作平行四边形MADB,则平行四边形MADB的对角线MD的最小值是3.
如图在△ABC中,∠BAC=30°,AB=AC=6,M为AC边上一动点(不与A,C重合),以MA、MB为一组邻边作平行四边形MADB,则平行四边形MADB的对角线MD的最小值是3.