题目内容

7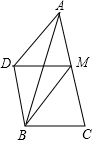．如图在△ABC中，∠BAC=30°，AB=AC=6，M为AC边上一动点（不与A，C重合），以MA、MB为一组邻边作平行四边形MADB，则平行四边形MADB的对角线MD的最小值是3．

分析 如图，作BH⊥AC于H．因为四边形ADBM是平行四边形，所以BD∥AC，所以当DM⊥AC时，DM的值最小，此时DM=BH．

解答 解：如图，作BH⊥AC于H．

在Rt△ABH中，∵AB=6，∠BHA=90°，∠BAH=30°，
∴BH=$\frac{1}{2}$AB=3，
∵四边形ADBM是平行四边形，
∴BD∥AC，
∴当DM⊥AC时，DM的值最小，此时DM=BH=3，
故答案为3．

点评 本题考查直角三角形30度角性质、等腰三角形的性质、平行四边形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．

练习册系列答案
相关题目
14．计算：$\sqrt{12}$+$\sqrt{16}$×$\sqrt{\frac{1}{8}}$-2sin45°+|2-$\sqrt{3}$|
18．“数形结合”和“建模思想”是数学中的两个很重要的思想方法，先阅读以下材料，然后解答后面的问题．
例：求代数式$\sqrt{{x}^{2}+{3}^{2}}+\sqrt{（12-x）^{2}+{2}^{2}}$的最小值．
解析：$\sqrt{{x}^{2}+{3}^{2}}$和$\sqrt{（12-x）^{2}+{2}^{2}}$是勾股定理的形式，$\sqrt{{x}^{2}+{3}^{2}}$是直角边分别是x和3的直角三角形的斜边，$\sqrt{（12-x）^{2}+{2}^{2}}$是直角边分别是12-x和2的直角三角形的斜边，因此，我们构造两个直角三角形△ABC和△DEF，并使直角边BC和EF在同一直线上（图1）向右平移直角三角形ABC使点B和E重合（图2），这时CF=x+12-x=12，AC=3，DF=2，问题就变成“点B在线段CF的何处时，AB+DB最短？”，根据两点间线段最短，得到线段AD就是它们的最小值．
小结：本题利用代数式$\sqrt{{x}^{2}+{3}^{2}}+\sqrt{（12-x）^{2}+{2}^{2}}$的形式特点，把它转化成为两个直角三角形的问题，从而利用已学过的几何知识来解决这个代数式问题，这就是建模思想与数形结合思想，回答下面问题：
（1）请你完成例题的解答；
（2）变式训练：求代数式$\sqrt{{x}^{2}+16}$+$\sqrt{（10-x）^{2}+4}$的最小值；
（3）拓展练习：解方程$\sqrt{9-{x}^{2}}$+$\sqrt{16-{x}^{2}}$=5（利用几何方法解答）
15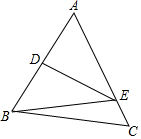．如图，在△ABC中，BC=4cm，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长等于9cm，则AC的长等于（　　）
A．3 cmB．4 cmC．5 cmD．6 cm
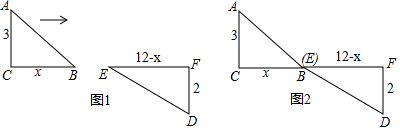
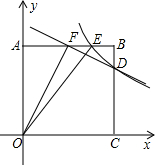2．如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4），与线段BC交于点D，直线y=-$\frac{1}{2}$x+b过点D，与线段AB相交于点F．
（1）求点F的坐标；
（2）连接OF、OE，探究∠AOF与∠EOC的数量关系，并证明；
（3）在x轴上找两点M，N，使MN=2，且使四边形AMND周长最小，求M，N两点的坐标．
12．矩形具有而菱形不一定具有的性质是（　　）
A．对角线互相平分B．对角线互相垂直C．对边相等D．对角线相等
19．某公司计划组装A、B两种型号的健身器材共40套，捐给社区健身中心．组装一套A型健身器材需甲种部件7个和乙种部件4个，组装一套B型健身器材需甲种部件3个和乙种部件6个，公司现在有甲种部件240个，乙种部件196个．
（1）公司在组装A、B两种型号的健身器材时，共有多少种组装方案？
（2）组装一套A型健身器材需费用20元，组装一套B型健身器材需费用18元，求总组装费用最少的组装方案，最少总组装费用是多少？
16．向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y=ax2+bx+c（a≠0）．若此炮弹在第6秒与
第14秒时的高度相等，则在第10秒时炮弹达到最大高度．
17．如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y=$\frac{k}{x}$的图象交于点D，且OD=2AD，过点D作x轴的垂线交x轴于点C．若S四边形ABCD=10，求此反比例函数的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网