题目内容
6.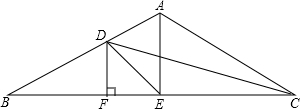 在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC=30°.
在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC=30°.
分析 过D作DM⊥AC交CA的延长线于M,DN⊥AE,根据角平分线的性质得到DF=DM,根据邻补角的定义得到∠DAM=60°,根据角平分线的定义得到∠BAE=60°,推出DE平分∠AEB,根据等腰三角形的性质得到∠AEB=90°,得到∠DEF=45°,根据三角形的外角的性质即可得到结论.
解答 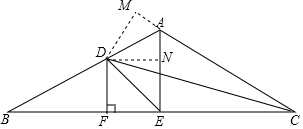 解:过D作DM⊥AC交CA的延长线于M,DN⊥AE,
解:过D作DM⊥AC交CA的延长线于M,DN⊥AE,
∵CD平分∠ACB,
∴DF=DM,
∵∠BAC=120°,
∴∠DAM=60°,
∵AE平分∠BAC,
∴∠BAE=60°,
∴∠DAM=∠BAE,
∴DM=DN,
∵DF⊥BC,
∴DE平分∠AEB,
∵AB=AC,AE平分∠BAC交BC于E,
∴AE⊥BC,
∴∠AEB=90°,
∴∠DEF=45°,
∵∠B=∠C=30°,
∴∠DCF=15°,
∴∠EDC=30°,
故答案为:30.
点评 本题考查了等腰三角形的性质,角平分线的性质,角平分线的定义,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.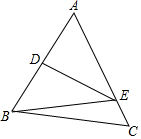 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 6 cm |
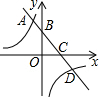 如图,已知函数y=-x+2的图象与x轴、y轴分别交于点C、B,与双曲线y=$\frac{k}{x}$交于点A、D,若AB+CD=BC,则k的值为-3.
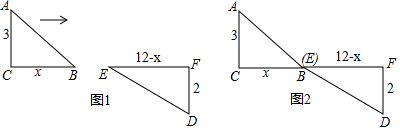
如图,已知函数y=-x+2的图象与x轴、y轴分别交于点C、B,与双曲线y=$\frac{k}{x}$交于点A、D,若AB+CD=BC,则k的值为-3. 如图:AC∥ED,∠A=∠EDF,试说明AB∥FD.
如图:AC∥ED,∠A=∠EDF,试说明AB∥FD.