题目内容
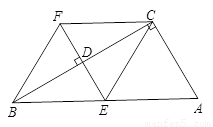
 已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=
已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE= (AB+AD),求证:∠B与∠D互补.
(AB+AD),求证:∠B与∠D互补.
 证明:在AB上截取AF=AD,连接CF,
证明:在AB上截取AF=AD,连接CF,∵AC平分∠BAD,
∴∠BAC=∠CAD,
又AC=AC,
∴△ACF≌△ACD(SAS),
∴AF=AD,∠AFC=∠D,
∵AE=
 (AB+AD),
(AB+AD),∴EF=BE,
又∵CE⊥AB,
∴BC=FC,
∴∠CFB=∠B,
∴∠B+D=∠CFB+∠AFC=180°,
即∠B与∠D互补.
分析:可在AB上截取AF=AD,可得△ACF≌△ACD,得出∠AFC=∠D,再由线段之间的关系AE=
 (AB+AD)得出BC=CF,进而通过角之间的转化即可得出结论.
(AB+AD)得出BC=CF,进而通过角之间的转化即可得出结论.点评:本题主要考查了全等三角形的判定及性质以及等腰三角形的判定及性质问题,能够熟练运用三角形的性质求解一些简单的计算、证明问题.

练习册系列答案
相关题目
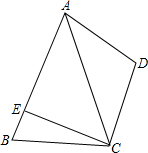 已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=
已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE= 已知如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2
已知如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2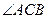 =90°
=90° ,
,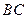 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. 的大小为多少度时,四边形BECF是正方形?
的大小为多少度时,四边形BECF是正方形?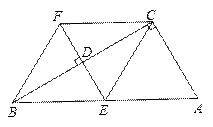
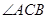 =90°,
=90°,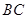 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. 的大小为多少度时,四边形BECF是正方形?
的大小为多少度时,四边形BECF是正方形?