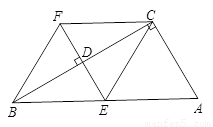
题目内容
 已知如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2
已知如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2(1)求证:AB=BC;
(2)过B作BF∥AC交CD的延长线于F,连EF,求证:AE=CF+EF.
分析:(1)由CD⊥AD,根据勾股定理得到AD2+CD2=AC2,而AD2+CD2=2AB2,则有AC2=2AB2,由∠ABC=90°,根据勾股定理得到AB2+BC2=AC2,则2AB2=AB2+BC2,即可得到结论;
(2)过B点作BH⊥AC于H,交AE于G点,由AB=AC,∠ABC=90°得到△ABC为等腰直角三角形,根据等腰直角三角形的性质得到∠3=∠4=∠5=45°,利用等角的余角相等
∠AGH=∠2+∠3,根据三角形外角性质有∠1=∠2;根据BF∥AC得∠6=∠3=45°,则∠4=∠6,然后根据三角形全等的判定方法可证得△ABG≌△CBF(ASA),
则AG=CF,BG=BF;也可证△BGE≌△BFE(SAS),则GE=EF,这样易得到结论.
(2)过B点作BH⊥AC于H,交AE于G点,由AB=AC,∠ABC=90°得到△ABC为等腰直角三角形,根据等腰直角三角形的性质得到∠3=∠4=∠5=45°,利用等角的余角相等
∠AGH=∠2+∠3,根据三角形外角性质有∠1=∠2;根据BF∥AC得∠6=∠3=45°,则∠4=∠6,然后根据三角形全等的判定方法可证得△ABG≌△CBF(ASA),
则AG=CF,BG=BF;也可证△BGE≌△BFE(SAS),则GE=EF,这样易得到结论.
解答:(1)证明:∵CD⊥AD,
∴∠ADC=90°,
∴AD2+CD2=AC2,
而AD2+CD2=2AB2,
∴AC2=2AB2,
∵∠ABC=90°,
∴AB2+BC2=AC2,
∴2AB2=AB2+BC2,
∴AB=BC;
(2)证明:过B点作BH⊥AC于H,交AE于G点,如图,
∵AB=AC,∠ABC=90°,
∴△ABC为等腰直角三角形,
∴∠3=∠4=∠5=45°,
∵∠AGH+∠GAH=90°,∠2+∠3+∠CAD=90°,
∴∠AGH=∠2+∠3,
而∠AGH=∠1+∠4,
∴∠1=∠2;
∵BF∥AC,
∴∠6=∠3=45°,
∴∠4=∠6,
∵在△ABG和△CBF中,
,
∴△ABG≌△CBF(ASA),
∴AG=CF,BG=BF,
∵在△BGE和△BFE中,
,
∴△BGE≌△BFE(SAS),
∴GE=EF,
而AE=AG+GE,
∴AE=CF+EF.

∴∠ADC=90°,
∴AD2+CD2=AC2,
而AD2+CD2=2AB2,
∴AC2=2AB2,
∵∠ABC=90°,
∴AB2+BC2=AC2,
∴2AB2=AB2+BC2,
∴AB=BC;
(2)证明:过B点作BH⊥AC于H,交AE于G点,如图,
∵AB=AC,∠ABC=90°,
∴△ABC为等腰直角三角形,
∴∠3=∠4=∠5=45°,
∵∠AGH+∠GAH=90°,∠2+∠3+∠CAD=90°,
∴∠AGH=∠2+∠3,
而∠AGH=∠1+∠4,
∴∠1=∠2;
∵BF∥AC,
∴∠6=∠3=45°,
∴∠4=∠6,
∵在△ABG和△CBF中,
|
∴△ABG≌△CBF(ASA),
∴AG=CF,BG=BF,
∵在△BGE和△BFE中,
|
∴△BGE≌△BFE(SAS),
∴GE=EF,
而AE=AG+GE,
∴AE=CF+EF.
点评:本题考查了全等三角形的判定与性质:有两组角对应相等,且它们所夹的边相等,那么这两个三角形全等;有两组边对应相等,且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等腰直角三角形的性质和勾股定理.

练习册系列答案
相关题目
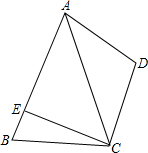 已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=
已知如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=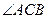 =90°
=90° ,
,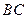 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.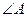 的大小为多少度时,四边形BECF是正方形?
的大小为多少度时,四边形BECF是正方形?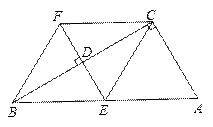
 =90°,
=90°,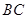 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.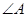 的大小为多少度时,四边形BECF是正方形?
的大小为多少度时,四边形BECF是正方形?